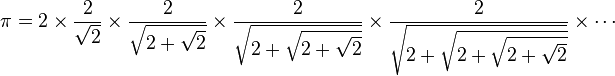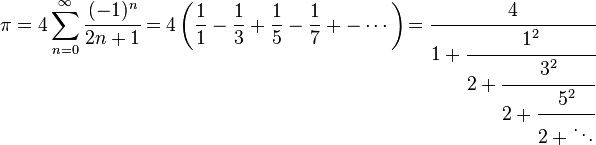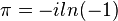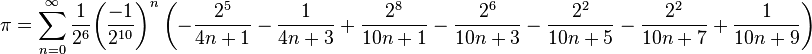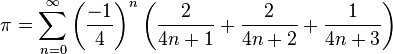Pi Sayısı Nedir? Pi Sayısı Ne Demektir? Anlamı, Tarihi ve Formülleri Nelerdir?

Özet: “Pi Sayısı Nedir? Pi Sayısı Ne Demektir? Anlamı, Tarihi ve Formülleri” başlıklı yazımızda Pi sayısı nedir, Pi sayısı ne demektir, Pi sayısı kelimesinin tanımı, Pi sayısı kelimesinin eş anlamlısı, Pi sayısı kelimesinin ingilizce karşılıkları, Pi sayısı tarihi, Pi Sayısı formülleri gibi Pi sayısı hakkında detaylı bilgileri bulacaksınız.

Sponsorlu Bağlantılar

Pi Sayısı Tanımı

Pi sayısı kelimesinin anlamı Türk Dil Kurumu (TDK) sözlüğünde aşağıdaki şekildedir;

isim, matematik Çember çevresinin uzunluğunun çapının uzunluğuna bölünmesi ile elde edilen sabit sayı (3,1416)

Pi Sayısı Eş Anlamlısı ve Zıt Anlamlısı

Pi sayısı kelimesini eş anlamlı karşılığı aşağıdaki gibidir;

Pi sayısı kelimesinin eş anlamlı karşılığı bulunmamaktadır.

Pi sayısı kelimesini zıt anlamlı karşılığı aşağıdaki gibidir;

Pi sayısı kelimesinin zıt anlamlı karşılığı bulunmamaktadır.

Pi Sayısı İle İlgili Atasözleri ve Deyimler

Pi sayısı kelimesi ile ilgili atasözü ve deyimler aşağıdaki gibidir;

Pi sayısı kelimesinin geçtiği herhangi bir atasözü veya deyim bulunamamıştır.

Pi Sayısı İle İlgili Birleşik Sözler

Pi sayısı kelimesi ile ilgili birleşik sözler aşağıdaki gibidir;

Pi sayısı kelimesinin geçtiği herhangi bir birleşik söz bulunamamıştır.

Pi Sayısı İngilizcesi

Pi sayısı kelimesinin İngilizce karşılıkları ise aşağıdaki gibidir

Pi sayısı – Pi

Pi Sayısı Hakkında Detaylı Bilgi

Pi sayısı ( $\pi$ ), bir dairenin çevresinin çapına bölümü ile elde edilen matematik sabiti. İsmini, Yunanca περίμετρον (çevre) sözcüğünün ilk harfi olan π den alır. Pi sayısı, Arşimet sabiti ve Ludolph sayısı olarak da bilinir.

Pi Sayısı Tarihi

Fabrice Bellard, 2010 yılında Chudnovsky algoritması kullanarak sayının ilk 2.699.999.990.000 basamağını bulmuştur. Arşimet, 3 tam 1/7 ile 3 tam 10/71 arasında bir sayı olarak hesapladı. Mısırlılar 3,1605, Babilliler 3.1/8, Batlamyus 3,14166 olarak kullandı. İtalyan Lazzarini 3,1415926, Fibonacci ise 3.141818 ile işlem yapıyordu.

Pi( $\pi$ ) Formülleri

Pi(π) formüllerinden başlıcaları şunlardır.

Nilakantha Somayaji:

$\pi={3}+{\frac{4}{{3^{3}}-3}}-{\frac{4}{{5^{3}}-5}}+{\frac{4}{{7^{3}}-7}}-{\frac{4}{{9^{3}}-9}}+...$

$\pi={3}+{\frac{4}{2\times3\times4}}-{\frac{4}{4\times5\times6}}+{\frac{4}{6\times7\times8}}-{\frac{4}{8\times9\times10}}+...$

Franciscus Vieta:

$\pi=2\times\frac{2}{\sqrt{2}}\times\frac{2}{\sqrt{2+\sqrt{2}}}\times\frac{2}{\sqrt{2+\sqrt{2+\sqrt{2}}}}\times\frac{2}{\sqrt{2+\sqrt{2+\sqrt{2+\sqrt{2}}}}}\times\cdots$

Gregory–Leibniz:

$\pi=4\sum_{n=0}^{\infty}\cfrac{(-1)^n}{2n+1}=4\left(\frac{1}{1}-\frac{1}{3}+\frac{1}{5}-\frac{1}{7}+-\cdots\right)\!=\cfrac{4}{1+\cfrac{1^2}{2+\cfrac{3^2}{2+\cfrac{5^2}{2+\ddots}}}}\!$

Isaac Newton:

$\pi=\sum_{n=0}^{\infty}\cfrac{{{2^{n+1}}\cdot{(n!)^2}}}{(2n + 1)!}$

Leonhard Euler:

$\pi=-iln(-1)$

Bailey-Borwein-Plouffe:

$\pi=\sum_{n=0}^{\infty}\biggl(\frac{1}{16}\biggr)^n\left(\frac{4}{8n+1}-\frac{2}{8n+4}-\frac{1}{8n+5}-\frac{1}{8n+6}\right)$

Fabrice Bellard:

$\pi=\sum_{n=0}^\infty\frac{1}{2^6}\biggl(\frac{-1}{2^{10}}\biggr)^n\left(-\frac{2^5}{4n+1}-\frac{1}{4n+3}+\frac{2^8}{10n+1}-\frac{2^6}{10n+3}-\frac{2^2}{10n+5}-\frac{2^2}{10n+7}+\frac{1}{10n+9}\right)\!$

Adamchik-Wagon:

$\pi=\sum_{n = 0}^{\infty}\biggl(\frac{-1}{4}\biggr)^n\left(\frac{2}{4n+1}+\frac{2}{4n+2}+\frac{1}{4n+3}\right)$