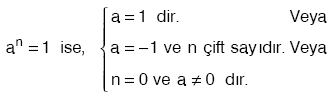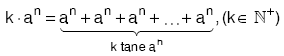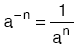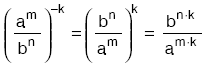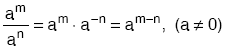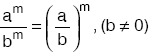Üslü Sayılar Ders Notu ve Konu Anlatımı

Üslü Sayılar

Üslü Sayılar konusu Matematik dersinin bilinmesi gereken ve hemen hemen tüm sorular da çıkabilecek temel konulardan birisidir. Üslü sayının tanımı, özellikleri, üslü sayılarda toplama, çıkarma, çarpma, bölme ve üslü sayılarda denklemler gibi alt başlıktan oluşan konularla hızlı bir şekilde öğrenebilirsiniz.

Üslü Sayılar konusunda dikkat etmeniz gereken nokta üslü sayıların özelliklerini kavrayabilmektir. Bu özellikleri bilmeden sorularda sıkıntı yaşayacağınızı bilmenizi isteriz. Aşağıda ki konu anlatımı ve ders notlarını iyi bir şekilde gözden geçirdikten sonra soruları kolay bir şekilde çözebileceksiniz.

A) ÜSLÜ SAYILARIN TANIMI:

a gerçel (reel) sayı ve n sayma sayısı olduğu düşünüldüğünde,

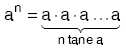
tanımına üslü ifade denir.

k × aⁿ ifadesinde k sayısına kat sayı, a ya taban, n ye üs denir.

B. ÜSLÜ İFADENİN ÖZELİKLERİ

1. a ¹ 0 ise, a⁰ = 1 dir.
2. 0⁰ tanımsızdır.
3. n Î R ise, 1ⁿ = 1 dir.
4. 
5. (a^m)ⁿ = (aⁿ)^m = a^m×n
6. 
7. 
8. Pozitif sayıların bütün kuvvetleri pozitiftir.
9. Negatif sayıların; çift kuvvetleri pozitif, tek kuvvetleri negatiftir.
10. n bir tam sayı ve a sıfırdan farklı bir gerçel (reel) sayı olmak üzere,

a) (–a)²ⁿ = a²ⁿ ifadesi daima pozitiftir.

b)(–a²ⁿ) = –a²ⁿ ifadesi daima negatiftir.

c) (–a)^{2n + 1} = –a^{2n + 1} ifadesi; a pozitif ise negatif, a negatif ise pozitiftir.

1. (n + 1) basamaklı  sayısı a × 10ⁿ ye eşittir.

x, n basamaklı olmak üzere,

C. ÜSLÜ İFADELERDE DÖRT İŞLEM

1. x × aⁿ + y × aⁿ – z × aⁿ = (x + y – z) × aⁿ
2. a^m× aⁿ = a^{m + n}
3. a^m× b^m = (a × b)^m
4. 
5. 

D. ÜSLÜ DENKLEMLER

1. a ¹ 0, a ¹ 1, a ¹ –1 olmak üzere,

a^x = a^y ise x = y dir

2. n, 1 den farklı bir tek sayı ve xⁿ = yⁿ ise, x  = y dir.

3. n, 0 dan farklı bir çift sayı ve xⁿ = yⁿ ise, x = y veya x = –y dir.

4.