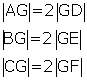Geometri dersinin üçgende kenarortay bağıntıları konusunda; ağırlık merkezinin ne demek olduğunu, ağırlık merkezi ile kenarortay arasındaki ilişkiyi, dik üçgende hipotenüs ve kenarortay ilişkisini, üçgenin alanı ile kenarortay ilişkisini, üçgenin uzunluğu ile kenarortay ilişkisini göreceğiz. Bu gibi özellikler ile bir üçgende kenarortay nasıl bulunur veya kenarortay özelliği ile bir üçgenin alanı ve uzunluğu nasıl bulunur gibi konuları öğreneceğiz.
Aşağıda üçgende kenarortay konusuna ait ders notu bulunmaktadır. Bu konu anlatımında üçgende kenarortay konusuna ait bilmeniz gereken tüm bilgiler vardır. Sizlerin yapacağı tek şey sadece iyi bir çalışmanın ardından hemen soru çözümüne başlamak olacaktır.
Üçgende Kenarortay
1. Ağırlık Merkezi
Üçgenlerde kenarortaylar bir noktada kesişirler.Kenarortayların kesişim noktasına ağırlık merkezi denir.
| ABC üçgeninde [AD], [BE] ve [CF] kenarortaylarının kesiştikleri G noktasına ABC üçgeninin ağırlık merkezi denir. | 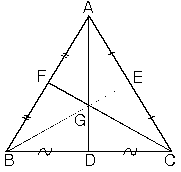 |
a. Ağırlık merkezi kenarortayı, kenara 1 birim, köşeye 2 birim olacak şekilde böler.
ABC üçgeninde D, E, F noktaları bulundukları kenarlarınorta noktaları ve G ağırlık merkezi ise
| 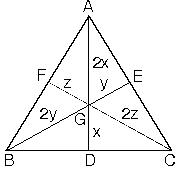 |
| b. Bir üçgende iki kenarortayın kesişmesiyle oluşan nokta ağırlık merkezidir. | 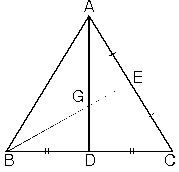 |
| c. ABC üçgeninde [AD] kenarortay ve|AG| = 2|GD| olduğundan G noktasıağırlık merkezidir. | 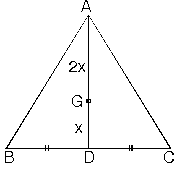 |
| d. ABC üçgeninde [AD] kenarortay ve |CG| = 2|FG|olduğundan G noktası ağırlık merkezidir. | 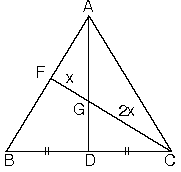 |
| e.ABC üçgeninde|AG| = 2|GD| ve |CG| = 2|GF|eşitliğini sağlayan G noktası ABCüçgeninin ağırlık merkezidir. | 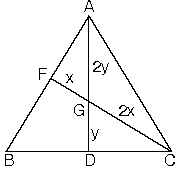 |
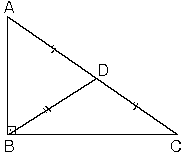
2. Dik üçgende hipotenüse ait kenarortay hipotenüsün yarısına eşittir.
ABC dik üçgeninde [BD] hipotenüse ait kenarortay
|  |
3. Kenarortayların Böldüğü Alanlar
| a.Kenarortaylar üçgenin alanını altı eşit parçaya bölerler. | 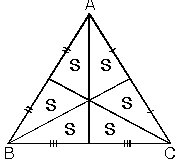 |
| b.G ağırlık merkezi köşelere birleştirildiğinde üçgenin alanı üç eşit parçaya bölünür. | 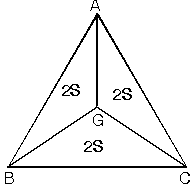 |
| c. G ağırlık merkezi kenarların orta noktaları ile birleştirildiğinde üçgenin alanı üç eşit parçaya bölünür. | 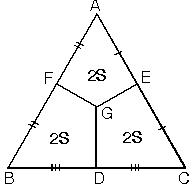 |
| 4.ABC üçgeninde kenarortaylar ve [FE] çizilirse|AK| = 3x|KG| = x|GD| = 2x eşitlikleri bulunur. | 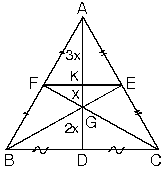 |
K noktası [AD] kenarortayının orta noktasıdır.
|
|
| a. ABC üçgeninde kenarortaylar ve [FE] çizildiğindeşekildeki gibi bir alan bölünmesi oluşur. | 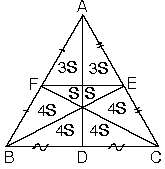 |
| b.Kenarların orta noktalarını birbirine birleştirdiğimizde üçgenin alanı dört eşit parçaya bölünür. | 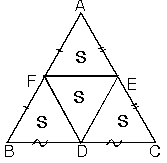 |
5. Kenarortay Uzunluğu
| ABC üçgeninde A köşesinden çizilen kenarortayın uzunluğuna Vadersek Bu bağıntı diğer kenarortaylar içinde geçerlidir. | 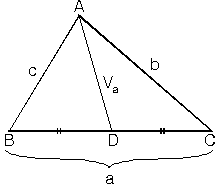 |
Kenarortaylar taraf tarafa toplanırsa
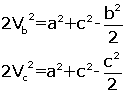
Kenarortaylar taraf tarafa toplanırsa
![]()
6. Dik Üçgende Kenarortaylar
| A açısı 90° olan bir dik üçgende kenarortaylar arasında | 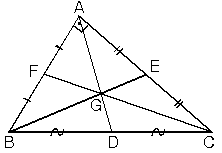 |