Paralelkenar Ders Notu ve Konu Anlatımı

Geometri dersinin Paralelkenar isimli konusunda; paralelkenarın tanımı, paralelkenarın alanı, paralelkenarın köşegen özelikleri gibi konuları göreceğiz. Paralelkenara ait şekiller ve özellikler sayesinde konuyu daha iyi kavrayacaksınız. Aşağıda bulunan paralelkenar konusunun ders notu ve konu anlatımına iyi bir şekilde çalıştıktan sonra soru çözümüne geçebilirsiniz. Soru çözümlerini kolaydan zora doğru yapmanızı tavsiye ediyoruz. Aksi takdir de henüz daha yeni soru çözmeye başlamışken motivasyon eksikliği yaşayabilirsiniz. Kolay sorularla konuya olan hakimiyetinizi arttırdıktan sonra diğer soruları daha kolay bir şekilde çözebileceksiniz. İyi çalışmalar dileriz.

Paralelkenar

Karşılıklı kenarları eşit ve paralel olan dörtgenlere paralelkenar denir.

[AB] // [DC][AD] // [BC]|AB| = |DC||AD| = |BC|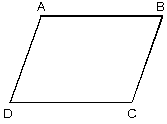

• Bir dörtgende karşılıklı kenarlar paralel ise eşit, eşit ise paralel olmak zorundadırlar.

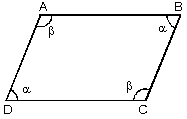
1. Paralelkenarda karşılıklı açılar eş, komşu açılar bütünlerdir. a + b = 180°

2. Paralelkenarın Alanı

a. Paralelkenarın alanı herhangi bir kenarla o kenara ait yüksekliğin çarpımına eşittir. A(ABCD) = a . ha = b . hb

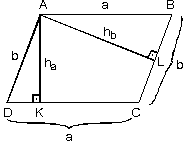b. İki kenarı ve bir açısının ölçüsü bilinen paralelkenarın alanı; A(ABCD) = a . b .sina

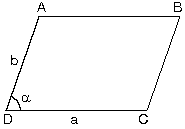c. Köşegen uzunlukları ve köşegenleri arasındaki açısının ölçüsü bilinen paralelkenarın alanı;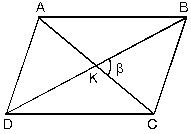

3. Paralelkenarda Köşegen Özellikleri

a. Paralelkenarda köşegenler birbirini ortalar. |AE| = |EC||DE| = |EB|

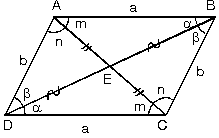b. Paralelkenarda köşegenler alanı dört eşit parçaya bölerler.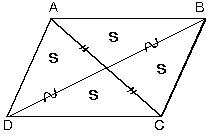

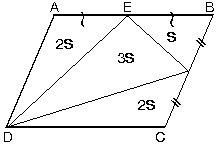
c. Paralelkenarda bir kenar üzerinde alınan bir noktanın karşı köşelere birleştirilmesiyle oluşan alan tüm alanın yarısına eşittir. A(PCD) = A(APD) + A(BPC)

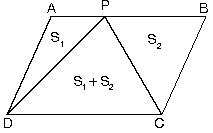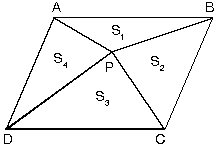
d. Paralelkenarın içinde alınan herhangi bir P noktası köşelere birleştirildiğinde oluşan karşılıklı üçgenlerin alanları toplamı eşittir. S1 + S3 = S3 + S4

Bir ABCD paralelkenarında bir köşeyi, karşı kenarların orta noktaları ile birleştirdiğimizde alanlar şekildeki gibi bölünür.

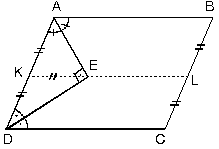
e. ABCD paralelkenarında K ve L noktaları kenarların orta noktaları olduğuna göre, E ABD üçgeninin, F de DCB üçgeninin ağırlık merkezidir.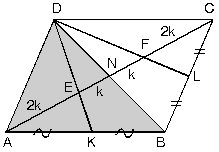
|AE| = 2|EN||FC| = 2|NF |AE| = |EF| = |FC|

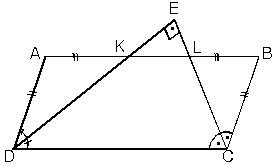
[AC] köşegeni, [DK] ve [DL] doğru parçaları paralelkenarın alanını şekildeki gibi bölerler.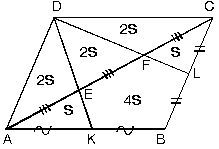

f. Paralelkenarda komşu iki açının açıortayları arasında kalan açı 90° dir.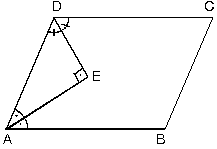

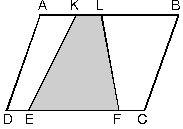
E noktasından [AB] ve [DC] kenarlarına çizilen paralel AED dik üçgeninde hipotenüse ait kenarortayın uzantısıdır. [AB] // [KL] // [DC] Û |AK| = |KD| = |KE| |BL| = |LC|

Açıortayların kesiştikleri noktanın paralelkenarın dışında kalması durumunda  |AD| = |AK| = |LB| = |BC|

g. ABCD paralelkanarının alanının taralı alana oranı; T.A/A(ABCD)= 1/2.(KL/AB+EF/DC)