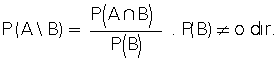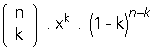Matematik dersinin Olasılık konusunda; Olasılığın tanımı nedir, deney nedir, sonuç nedir, örnek ve ve örnek nokta nedir, olay nedir, imkansız olay ve mutlak olay nedir, ayrık olay nedir, olasılık fonksiyonu nedir gibi sorulara yanıt arayacağız. Bunun yanı sıra bağımsız ve bağımlı olaylar ile koşullu olasılık başlıklarına göz atacağız.
Aşağıda Olasılık konusuna ait ders notu ve konu anlatımı bulunmaktadır. Olasılık konusuyla ilgili bütün bilgileri aşağıda bulabilirsiniz. Konu anlatımına iyi bir şekilde çalıştıktan sonra soru çözümlerine başlayabilirsiniz. İyi çalışmalar.
Olasılık
A. TANIM
Olasılık, sonucu kesinlik kazanmayan durumlarla ilgilidir. Bir zar atıldığı zaman zarın nereye geleceği noktaların sayısının ne olacağı gibi şans oyunlarıyla ilgilenen olasılık teorisi günümüzde sosyal durumlar ve bilimsel araştırmalar da kullanılmaktadır.
B. OLASILIK TERİMLERİ
Bir madeni para yukarıya atıldığında yazı mı ya da tura mı geleceğini (v.b) tespit etme olayına deney denir.
Bir deneyin her bir görüntüsüne (çıktısına) sonuç denir.
Bir deneyin bütün sonuçlarını eleman kabul eden kümeye örnek uzay ve örnek uzayın her bir elemanına örnek nokta denir.
Bir örnek uzayın her bir alt kümesine olay denir.
Örnek uzayın alt kümelerinden olan boş kümeye imkansız (olanaksız) olay denir.
Örnek uzayın bütün elemanlarını içeren alt kümesine mutlak (kesin) olay denir.
A ve B, E örnek uzayına ait iki olay olsun.
ise, A ve B olayına ayrık olay denir. |
C. OLASILIK FONKSİYONU
E örnek uzayının bütün alt kümelerinin oluşturduğu kuvvet kümesi K olsun.
P : K ® [0, 1]
biçiminde tanımlanan P fonksiyonuna olasılık fonksiyonu denir. A Î K ise P(A) gerçel sayısına A olayının olasılığı denir.
Ü 1) Her A Î K için, 0 £ P(A) £ 1 dir. Yani, A olayının olasılığı 0 ile 1 arasındadır.
2) İmkansız olayın olasılığı 0 ve kesin olayın olasılığı 1 dir.
3) A, B Î K ve A Ç B = Æ ise,
P(A È B) = P(A) + P(B) dir.
| 1) |  |
2) A Ì B ise P(A) £ P(B) dir.
3) A, A nın tümleyeni olmak üzere,
P(A) + P(–A) = 1 dir.
4) P(A È B) = P(A) + P(B) – P(A Ç B)
5) A, B, C olayları E örnek uzayının ikişer ikişer ayrık bütün olayları ise,
(E = A È B È C)
P(A) + P(B) + P(C) = 1 dir.
Ü 1) n, paranın atılma sayısını veya para sayısını göstermek üzere, örnek uzay 2n
dir.
Ü 2) n, zarın atılma sayısını veya zar sayısını göstermek üzere, örnek uzay 6n dir.
D. BAĞIMSIZ VE BAĞIMLI OLAYLAR
Bir olayın elde edilmesi, diğer olayın elde edilmesini etkilemiyorsa bu iki olaya bağımsız olaylar denir.
Eğer iki olay bağımsız değil ise, bu olaylara birbirine bağımlıdır denir.
Ü A ve B bağımsız iki olay olsun. A nın ve B nin gerçekleşme olasılığı :
P(A Ç B) = P(A) . P(B) dir.
E. KOŞULLU OLASILIK
A ve B, E örnek uzayında iki olay olsun. B olayının gerçekleşmiş olması durumunda, A olayının olasılığına, A olayının B ye bağlı koşullu olasılığı denir ve P(A B) ile gösterilir.
Bir deneyde bir A olayının olasılığı x olsun. Bu deney n kez tekrarlandığında A olayının k kez gerçekleşmesi olasılığı,