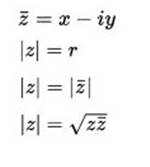Mutlak Değer Ne Demektir?
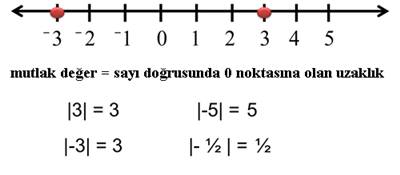
Matematik alanında kullanılan mutlak değer, gerçek bir sayının işaretsiz değerini verendir. Örnek olarak verirsek; 9 sayısı hem 9’un hemde -9’un mutlak değeridir. En kısa tabirle mutlak değer, bir sayının sıfıra olan uzaklığıdır. Mutlak değer karmaşık sayılarda da kullanılabilir.
Mutlak değer özelliklerini, gerçek sayılarda olduğu gibi karmaşık sayılarda doğrudan uygulayamazsınız. Eğer Önerme 1’i örnek alırsak;
Ι a Ι = √a²
her gerçel sayının bir karmaşık sayı olduğunu ve bir karmaşık sayının da;
z = x + i*y
olduğunu kabul edersek; göreceğiz ki, gerçel sayılarda y katsayısı 0’a eşittir. Buna göre z’nin mutlak değerini (ya da karmaşık sayılarda bazen modül olarak isimlendirilir) şöyle tanımlayabiliriz;
Ι x + i*0 Ι = √x²+0² = √x² = Ι x Ι
Mutlak değer demek bir sayının orjinaline olan uzaklığıdır.
Karmaşık Sayılar
Karmaşık sayılar 2 boyutlu üzerinden incelenir ve bu nedenle Pisagor teoremi kullanılır. Karmaşık düzlemde 2 nokta arasındaki bulmak için aynı gerçel sayılarda;
z = x + i*y = r (cos ∅+ i* sin ∅) ise ve z karmaşık sayısının eşlenik’i ise;