Modüler Artimetik konusu Matematik dersinin kısa konularından birisidir. Parantez içinde mod yazılarak gösterilen bu konuya aslında çok yabancı değiliz. Kısa olan konuların öğrenilmesi de kolay olduğu için Modüler Artimetik konusundan korkmanıza gerek yoktur.
Ders notu ve konu anlatımı olarak sizler için derlediğimiz aşağıda ki yazıya iyi bir şekilde çalıştıktan sonra soru çözümlerine başlayabilecek ve soruları çözerken hiç bir şekilde zorlanmayacaksınız.
MODÜLER ARİTMETİK
a, b, m birer tam sayı ve m > 1 olmak üzere, tam sayılar kümesi üzerinde tanımlanan,
b = {(a, b) : m, (a – b) yi tam böler}
bir denklik bağıntısıdır.
b denklik bağıntısı olduğundan
Her (a, b) Î b için,
a º b (mod m)
biçiminde yazılır ve m modülüne göre a sayısı b ye denktir denir.
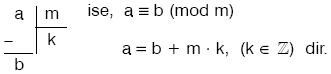 |
Tam sayıların m sayma sayısı ile bölünmesiyle elde edilen kalanlar, 0, 1, 2, 3, 4, … , (m – 1) dir.
Her tam sayı m ile bölündüğünde hangi kalanı veriyorsa o kalana denktir. Bu kalanların her biri, belirlediği denklik sınıfının temsilci elemanı olarak alınırsa, denklik sınıfları
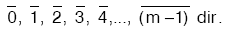
Bu denklik sınıflarının kümesine m nin kalan sınıflarının kümesi denir ve 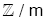 biçiminde gösterilir.
biçiminde gösterilir.
Buna göre,
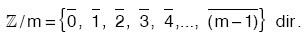
| n bir sayma sayısı ve k bir tam sayı ve a ºb (mod m) c º d (mod m)olmak üzere, |
- a + c º b + d (mod m)
- a – c º b – d (mod m)
- a × c º b × d (mod m)
- an º bn (mod m)
- a – b º 0 (mod m)
- k × a º k × b (mod m) dir.
- n sayma sayısı; a, b, m sayılarının ortak böleni ise
 dir.
dir. - a ile m ve b ile m aralarında asal olmak üzere,
 dir.
dir.
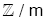 deki işlemler (mod m) ye göre yapılır. deki işlemler (mod m) ye göre yapılır. |
| Ü x, m nin tam katı olmayan pozitif bir tam sayı ve m bir asal sayı ise, xm–1 º1 (mod m) dir.x in (m – 1) den daha küçük kuvvetinde de 1 bulunabilir. | |
x ile m aralarında asal sayılar olmak üzere, m nin asal çarpanlarının kuvvetleri biçiminde yazılmış hâli m = ak . b r . c p olmak üzere,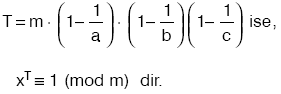 |

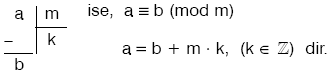
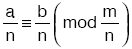 dir.
dir.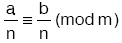 dir.
dir.