Matematik dersinin Modüler Aritmetik konusunda; Modüler Aritmetiğin tanımı, denklik bağıntısı, denklik sınıfları ve Modüler Aritmetiğin nasıl gösterildiği gibi konuları göreceğiz. Aşağıda Modüler Aritmetik konusuna ait ders notu ve konu anlatımı bulunmaktadır. Modüler Aritmetik ile ilgili bilmeniz gereken bütün bilgiler aşağıda bulunmaktadır. Hızlı bir şekilde konu anlatımına çalıştıktan sonra hemen soru çözümlerine başlayarak öğrenmenizi kalıcı hale getirebilirsiniz. İyi çalışmalar dileriz.
Modüler Aritmatik
MODÜLER ARİTMETİK
a, b, m birer tam sayı ve m > 1 olmak üzere, tam sayılar kümesi üzerinde tanımlanan,
b = {(a, b) : m, (a – b) yi tam böler}
bir denklik bağıntısıdır.
b denklik bağıntısı olduğundan
Her (a, b) Î b için,
a º b (mod m)
biçiminde yazılır ve m modülüne göre a sayısı b ye denktir denir.
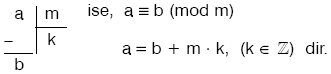 |
Tam sayıların m sayma sayısı ile bölünmesiyle elde edilen kalanlar, 0, 1, 2, 3, 4, … , (m – 1) dir.
Her tam sayı m ile bölündüğünde hangi kalanı veriyorsa o kalana denktir. Bu kalanların her biri, belirlediği denklik sınıfının temsilci elemanı olarak alınırsa, denklik sınıfları
![]()
Bu denklik sınıflarının kümesine m nin kalan sınıflarının kümesi denir ve Z/m biçiminde gösterilir.
Buna göre,
![]()
| n bir sayma sayısı ve k bir tam sayı ve a ºb (mod m) c º d (mod m)olmak üzere, |
- a + c º b + d (mod m)
- a – c º b – d (mod m)
- a × c º b × d (mod m)
- an º bn (mod m)
- a – b º 0 (mod m)
- k × a º k × b (mod m) dir.
- n sayma sayısı; a, b, m sayılarının ortak böleni ise
 dir.
dir. - a ile m ve b ile m aralarında asal olmak üzere,
 dir.
dir.
| Z/m deki işlemler (mod m) ye göre yapılır. |
| Ü x, m nin tam katı olmayan pozitif bir tam sayı ve m bir asal sayı ise, xm–1 º1 (mod m) dir.x in (m – 1) den daha küçük kuvvetinde de 1 bulunabilir. | |
x ile m aralarında asal sayılar olmak üzere, m nin asal çarpanlarının kuvvetleri biçiminde yazılmış hâli m = ak . b r . c p olmak üzere, 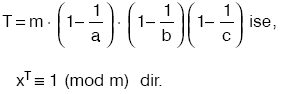 |
| m asal sayı ise, (m – 1)! + 1º 0 (mod m) dir. |
