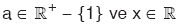Matematik dersinin Logaritma konusunda; üstel fonksiyonlar ve logaritmik fonksiyonlar, logaritma fonksiyonunun özellikleri, onluk logaritma fonksiyonunun özellikleri, doğal logaritma fonksiyonu, logaritmalı denklemler, logaritmalı eşitsizlikler konularını göreceğiz.
Aşağıda Logaritma konusuna ait ders notu ve konu anlatımı bulunmaktadır. Logaritma ile ilgili bilinmesi gereken bütün bilgiler aşağıdaki yazımızda vardır. İyi çalışmalar dileriz.
Logaritma
I. ÜSTEL FONKSİYONLAR VE LOGARİTMİK FONKSİYONLAR
2y = 24 eşitliğini sağlayan y değerini bulmak için yapılan işleme üslü denklemi çözme denir. (y = 4)
Buraya kadar anlatılan bilgiler 6a = 10 eşitliğini sağlayan a değerini bulmak için yeterli değildir. Bu eşitliği sağlayan a değerini bulmak için yapılan işleme logaritma alma denir.
A. ÜSTEL FONKSİYONLAR
olmak üzere,
biçiminde tanımlanan fonksiyona üstel fonksiyon adı verilir.
a > 0 olduğundan f(x) = ax > 0 olur.
B. LOGARİTMA FONKSİYONU
olmak üzere,
biçiminde tanımlanan üstel fonksiyonun ters fonksiyonuna logaritma fonksiyonu denir.
şeklinde gösterilir. Buna göre,
dir.
y = logax ifadesinde 
sayısına 
sayısının a tabanına göre logaritması denir ve ‘‘y eşittir a tabanına göre logaritma x ’’ şeklinde okunur.
C. LOGARİTMA FONKSİYONUNUN ÖZELLİKLERİ
Kural
1 den farklı her a pozitif reel sayısının a tabanına göre logaritması 1 dir. Buna göre,  |
Kural
Her tabana göre, 1 in logaritması 0 dır. Buna göre,  |
Kural
 |
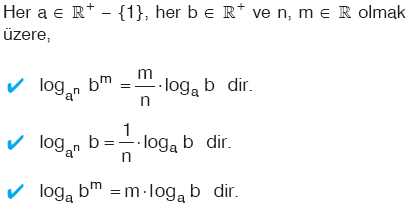Kural
 |
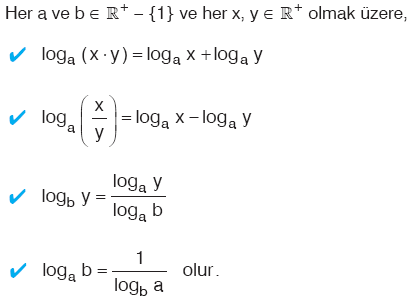Kural
 |
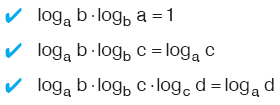Kural
 |
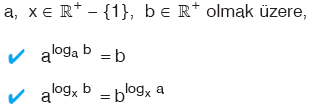D. ONLUK LOGARİTMA FONKSİYONU
f(x) = logax fonksiyonunda taban a = 10 alınırsa f(x) fonksiyonuna onluk logaritma fonksiyonu denir ve kısaca logx biçiminde gösterilir.
1 den büyük sayıların on tabanına göre logaritması pozitiftir.
1 den küçük pozitif sayıların on tabanına göre logaritması negatiftir.
Kural
| x > 1 olmak üzere, x in onluk logaritmasının tam kısmı, x in basamak sayısının bir eksiğine eşittir. 0 < y < 1 olmak üzere, y nin ondalık kesir biçiminde yazılışında, sıfırdan farklı ilk rakamın solundaki sıfır sayısı K ise, logy nin eşitinin tam kısmı –(K – 1) dir. |
E. DOĞAL LOGARİTMA FONKSİYONU
f(x) = logax fonksiyonunda taban
ℓ = 2,718281828459045235360287471352… alınırsa (ℓ sayısı irrasyonel bir sayı olup yaklaşık değeri 2,718 kabul edilir.) doğal logaritma fonksiyonu elde edilir. Doğal logaritma fonksiyonu kısaca lnx biçiminde gösterilir. Bu durumda,
İşlemlerde genellikle logex yerine lnx ifadesi kullanılır.
II. LOGARİTMALI DENKLEMLER
Özellik
| a sayısı 1 sayısından farklı bir pozitif sayı olmak üzere, tabanı a olan logaritmalı denklem, logaf(x) = b ise f(x) = abdir. logaf(x) = logag(x) ise f(x) = g(x) dir.Logaritmalı denklemleri bu özellikleri kullanarak çözeriz. Logaritmanın tanımından, f(x) > 0 ve g(x) > 0 olmalıdır. |
III. LOGARİTMALI EŞİTSİZLİKLER
Kural
| logaf(x) in işareti a ya bağlı olduğundan eşitsizlik çözümlerinde aşağıdaki bilgileri kullanırız.
|
