Matematik dersinin Limit ve Süreklilik konusunda; Limitte soldan yaklaşma ve sağdan yaklaşma, limit kavramı, uç noktalardaki limit, limitle ilgili özellikler, parçalı fonksiyonun limiti, işaret fonksiyonun limiti, tam değer fonksiyonun limiti, trigonometrik fonksiyonların limiti, belirsizlik durumları, süreklilik kavramı, L’Hospital kuralı konularını göreceğiz.
Limit ve süreklilik konusu biraz uzun olduğu için gözünüzü korkutmasın. Limit ve süreklilik konusu Türev ve İntegral konularına zemin hazırlayan bir konudur. O yüzden bu konuyla ilgili eksikliklerinizin olmamasına gayret gösterin. Aşağıda limit ve süreklilik konusuna ait ders notu ve konu anlatımı bulunmaktadır. Limit ve süreklilik konusuyla ilgili bilmeniz gereken bütün bilgileri bu sayfada bulabilirsiniz. İyi çalışmalar dileriz.
1. Limit
LİMİT
A. SOLDAN YAKLAŞMA, SAĞDAN YAKLAŞMA
x değişkeni a ya, a dan küçük değerlerle yaklaşıyorsa, bu tür yaklaşmaya soldan yaklaşma denir ve ![]() biçiminde gösterilir.
biçiminde gösterilir.
x değişkeni a ya, a dan büyük değerlerle yaklaşıyorsa, bu tür yaklaşmaya sağdan yaklaşma denir ve ![]() biçiminde gösterilir.
biçiminde gösterilir.
B. LİMİT KAVRAMI
Limit kavramını bir fonksiyonun grafiği üzerinde açıklayalım:
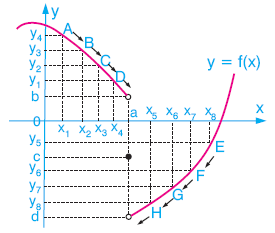
Grafiği verilen y = f(x) fonksiyonu için, apsisleri; x = a nın solunda yer alan ve giderek a ya yaklaşan A(x1, y4) , B(x2, y3) , C(x3, y2) , D(x4, y1), … noktalarını göz önüne alalım:
Bu noktaların apsisleri olan x1, x2, x3, x4, … giderek a ya yaklaşırken, ordinatları
f(x1) = y4, f(x2) = y3, f(x3) = y2, f(x4) = y1, … giderek b ye yaklaşır.
Bu durumu; x, a ya soldan yaklaşıyorken f(x) b ye yaklaşır şeklinde ifade edebiliriz. Bu durumda,
f(x) in x = a daki soldan limiti b dir denir. Ve
![]()
şeklinde gösterilir.
Yukarıdakine benzer şekilde, apsisleri x = a nın sağında yer alan ve giderek a ya yaklaşan
E(x8, y5) , F(x7, y6) , G(x6, y7) , H(x5, y8) , … noktalarını göz önüne alalım.
Bu noktaların apsisleri olan x8, x7 , x6 , x5 , … giderek a ya yaklaşırken, ordinatlar f(x8) = y5 , f(x7) = y6 , f(x6) = y7 , f(x5) = y8 , … giderek d ye yaklaşır.
Bu durumu “x, a ya sağdan yaklaşıyorken f(x) d ye yaklaşır.” şeklinde ifade edebiliriz.
Bu durumda; f(x) in x = a daki sağdan limiti d dir denir. Ve
![]()
biçiminde gösterilir.
Kural
| f(x) fonksiyonunun x = a daki soldan limiti sağdan limitine eşit ise fonksiyonun x = a da limiti vardır ve x in a noktasındaki limiti L ise, |
C. UÇ NOKTALARDAKİ LİMİT
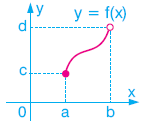
f fonksiyonu [a, b) aralığından [c, d) aralığına tanımlı olduğu için, uç noktalardaki limitleri araştırılırken, sadece tanımlı olduğu tarafın limitine bakılarak sonuca gidilir.
Fonksiyonun bir noktada limitinin olması için, o noktada tanımlı olması zorunlu değildir. Buna göre,
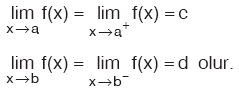
Kural
a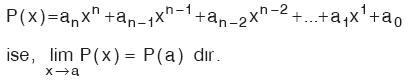 |
D. LİMİTLE İLGİLİ ÖZELLİKLER
Özellik
f ve g , x = a da limitleri olan iki fonksiyon olsun. 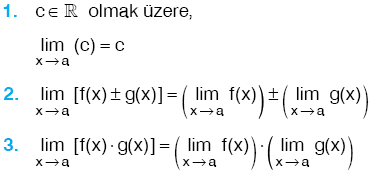 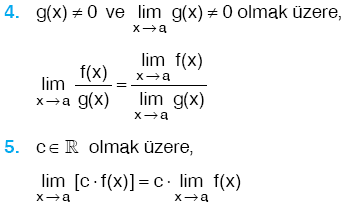 |
Özellik
Özellik
 |
Özellik
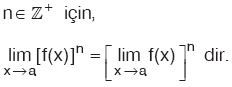 |
Özellik
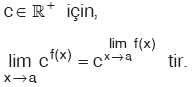 |
Özellik
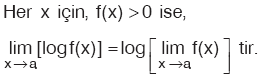 |
E. PARÇALI FONKSİYONUN LİMİTİ
Özellik
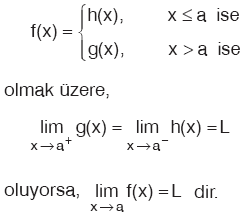 |
F. İŞARET FONKSİYONUNUN LİMİTİ
Özellik
f(x) = sgn [g(x)] olsun.  Bu sonuç genellikle doğrudur. Fakat az da olsa bu sonuca uymayan örnekler vardır.Söz gelimi, f(x) = sgn(x2) fonksiyonunun x = 0 da limiti vardır ve 1 dir. |
G. TAM DEĞER FONKSİYONUNUN LİMİTİ
Özellik
 Bu sonuç genellikle doğrudur. Fakat az da olsa bu sonuca uymayan örnekler vardır.Söz gelimi, Bu sonuç genellikle doğrudur. Fakat az da olsa bu sonuca uymayan örnekler vardır.Söz gelimi, |
H. ![]() NİN x = a DAKİ LİMİTİ
NİN x = a DAKİ LİMİTİ
Özellik
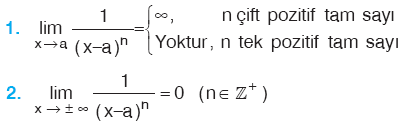 |
I. TRİGONOMETRİK FONKSİYONLARIN LİMİTİ
1. sinx in ve cosx in limiti
sinx ve cosx fonksiyonu bütün x reel değerleri için tanımlı olduğu için,
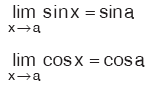
olur.
2. tanx in limiti
tanx fonksiyonu k£Z olmak üzere,
![]() koşuluna uyan bütün x reel değerleri için tanımlı olduğu için,
koşuluna uyan bütün x reel değerleri için tanımlı olduğu için,
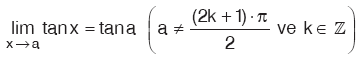
olur.
Sonuç
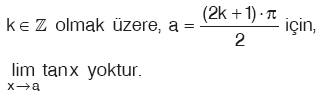 |
3. cotx in limiti
cotx fonksiyonu k£Z olmak üzere, ![]() koşuluna uyan bütün x reel değerleri için tanımlı olduğu için,
koşuluna uyan bütün x reel değerleri için tanımlı olduğu için,
![]()
olur.
Sonuç
 |
J. BELİRSİZLİK DURUMLARI
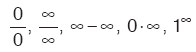
belirsizlikleriyle karşılaştığımızda aşağıda verilen yöntemler kullanılarak limit hesaplanır. Bu limitler türevin içinde vereceğimiz L’Hospital kuralıyla da hesaplanabilir.
Kural
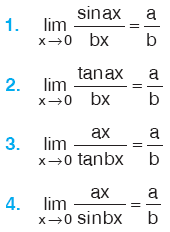 |
Kural
m, n Î N olmak üzere, 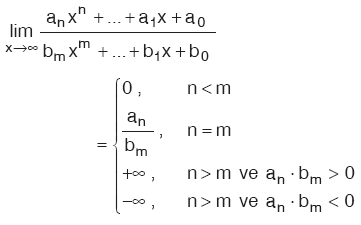 olur. olur. |
Kural
a > 0 olmak üzere, ¥ – ¥ belirsizliği olan limitler, 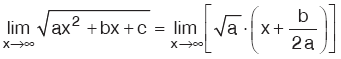 kuralını kullanarak hesaplanabilir. kuralını kullanarak hesaplanabilir. |
Kural
 Buna göre, 0 × ¥ belirsizliği 0/0 veya sonsuz/sonsuz belirsizliğine dönüştürülerek sonuca gidilir. Buna göre, 0 × ¥ belirsizliği 0/0 veya sonsuz/sonsuz belirsizliğine dönüştürülerek sonuca gidilir. |
Kural
a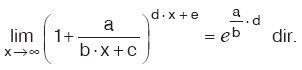 |
2. Süreklilik
Kural
| |
Sonuç
| y = f(x) fonksiyonu x = a da sürekli ise, |
Uyarı
| f(x) fonksiyonu apsisi x = a olan noktada sürekli değil ise, süreksizdir. |
Kural
| 1. Bir fonksiyon bir noktada tanımsız ise, o noktada süreksizdir. 2. Bir fonksiyon bir noktada limitsiz ise, o noktada süreksizdir. 3. Bir fonksiyon bir noktada tanımlı ve limitli ancak, tanım değeri limit değerinden farklı ise, bu noktada süreksizdir. |
A. L’HOSPİTAL KURALI
Bir fonksiyonun x = a noktasındaki limiti hesaplanırken karşımıza çıkan,
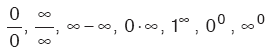
belirsizlikleri, 0/0 veya sonsuz bölü sonsuz belirsizliklerinden birine dönüştürülerek,
L’ Hospital Kuralı yardımıyla sonuçlandırılır.
Kural
f ve g, (a, b) aralığında türevlenebilir olsun. Her x Î (a, b) için g’(x) ¹ 0 ve c Î (a, b) olmak üzere,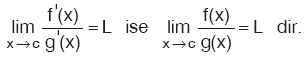 Eğer, Eğer, 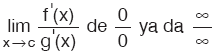 ise yukarıdaki kural bir ise yukarıdaki kural birdaha uygulanır. |
Uyarı
| L’ Hospital kuralında 0/0 veya sonsuz bölü sonsuz belirsizliğini ortadan kaldırmak için, yapılan işlemin: Payın türevini paya, paydanın türevini paydaya yazmak olduğuna dikkat ediniz. |
Kural
Sonusz × 0 belirsizliğinde,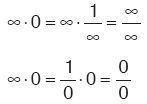 düzenlemelerinden biriyle sonuca gidilir. ¥– ¥ belirsizliğinde, 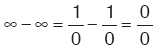 düzenlemesiyle sonuca gidilir. 00, ¥ , 1¥ belirsizliklerinde, e tabanında logaritma alınarak sonuca gidilir. |
