Matematiğin kümeler adlı bölümünde; kümenin tanımı, kümelerin gösterilişi, liste yöntemi, ortak özellik yöntemi, şema yöntemi, eşit küme, denk küme, boş küme, alt küme, özalt küme, kümelerde yapılan işlemler, birleşim işlemi, kesişim işlemi, evrensel küme, bir kümenin tümleyeni, kuvvet kümesi, iki kümenin farkı gibi konular bulunmaktadır. Gördüğünüz gibi kümeler bölümü ayrıntılı ve uzun bir konudur.
Aşağıda sizler için derlediğimiz kümeler ders notu ve konu anlatımına iyi bir şekilde çalışırsınız soru çözümlerinde zorlanmayacak ve soruları çok kolay bir şekilde çözebileceksiniz. Kümeler konusuyla ilgili bilmeniz gereken bütün bilgiler aşağıda verilmişti.
A. TANIM
- Küme, nesnelerin iyi tanımlanmış listesidir.
- Kümeler genellikle A, B, C gibi büyük harflerle gösterilir.
- Kümeyi oluşturan ögelere, kümenin elemanı denir. a elemanı A kümesine ait ise, a Î A biçiminde yazılır. “a, A kümesinin elemanıdır.” diye okunur. b elemanı A kümesine ait değilse, b Ï A biçiminde yazılır. “b, A kümesinin elemanı değildir.” diye okunur.
- Kümede, aynı eleman bir kez yazılır.
- Elemanların yerlerinin değiştirilmesi kümeyi değiştirmez.
- A kümesinin eleman sayısı s(A) ya da n(A) ile gösterilir.
B. KÜMELERİN GÖSTERİLİŞİ
Kümenin elemanları aşağıdaki 3 yolla gösterilebilir.
1. Liste Yöntemi
Kümenin elemanları { } sembolü içine, her bir elemanın arasına virgül konularak yazılır.
A = {a, b, {a, b, c}} ise, s(A) = 3 tür.
2. Ortak Özelik Yöntemi
Kümenin elemanlarını, daha somut ya da daha kolay algılanır biçimde gerektiğinde sözel, gerektiğinde matematiksel bir ifade olarak ortaya koyma biçimidir.
A = {x : (x in özeliği)}
Burada “x :” ifadesi “öyle x lerden oluşur ki” diye okunur.
Bu ifade “x |” biçiminde de yazılabilir.
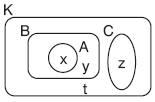
3. Şema Yöntemi
Küme, kapalı bir eğri içinde her eleman bir nokta ile gösterilip noktanın yanına elemanın adı yazılarak gösterilir.
Bu gösterime Venn Şeması ile gösterim denir.
C. EŞİT KÜME, DENK KÜME
Aynı elemanlardan oluşan kümelere eşit kümeler denir. Eleman sayıları eşit olan kümelere denk kümeler denir.
A kümesi B kümesine eşit ise A = B,
C kümesi D kümesine denk ise C º D
biçiminde gösterilir.
| Eşit olan kümeler ayın zamanda denktir. Fakat denk kümeler eşit olmayabilir. |
D. BOŞ KÜME
Hiç bir elemanı olmayan kümeye boş küme denir.
Boş küme { } ya da Æ sembolleri ile gösterilir.
| {Æ} ve {0} kümeleri boş küme olmayıp birer elemana sahip iki denk kümedir. |
E. ALT KÜME – ÖZALT KÜME
A kümesinin her elemanı, B kümesinin de elemanı ise A ya B nin alt kümesi denir.
1. Alt Küme
A kümesi B kümesinin alt kümesi ise A Ì B biçiminde gösterilir.
A kümesi B kümesinin alt kümesi ise B kümesi A kümesini kapsıyor denir. B É A biçiminde gösterilir.
C kümesi D kümesinin alt kümesi değilse C Ë D biçiminde gösterilir.
2. Özalt Küme
Bir kümenin, kendisinden farklı bütün alt kümelerine o kümenin özalt kümeleri denir.
3. Alt Kümenin Özelikleri
Her küme kendisinin alt kümesidir.
i) A Ì A
ii) Boş küme her kümenin alt kümesidir.
Æ Ì A
iii) (A Ì B ve B Ì A) Û A = B dir.
ıv) (A Ì B ve B Ì C) ise, A Ì C dir.
v) n elemanlı bir kümenin alt kümelerinin sayısı 2n ve özalt kümelerinin sayısı 2n – 1 dir.
| – | Elemanları arasında a bulunan n elemanlı bir kümenin,• alt kümelerinden 2n–1tanesinde a bulunmaz.• alt kümelerinden 2n–1 tanesinde a bulunur. |
n elemanlı bir kümenin r tane (n ³ r) elemanlı alt kümelerinin sayısı, 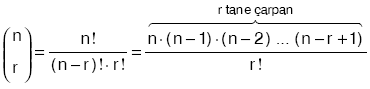 dir. dir. |
n elemanlı bir kümenin 0 elemanlı (boş küme) ve n elemanlı alt kümeleri sayısı 1 dir. 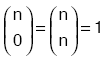 |
n elemanlı bir kümenin 1 elemanlı ve n – 1 elemanlı alt kümeleri sayısı n dir. 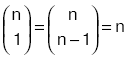 |
n elemanlı bir kümenin; x elemanlı alt kümeleri sayısı, y elemanlı alt kümeleri sayısına eşit ise, x = y veya n = x + y dir. 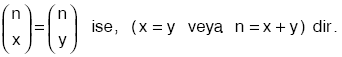 |
n elemanlı bir kümenin bütün alt kümeleri sayısı 2n olduğu için, 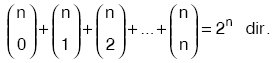 |
F. KÜMELERLE YAPILAN İŞLEMLER
A nın elemanlarından veya B nin elemanlarından oluşan kümeye bu iki kümenin birleşim kümesi denir ve A ÈB biçiminde gösterilir.
1. Kümelerin Birleşimi
A È B = {x : x Î A veya x Î B} dir.
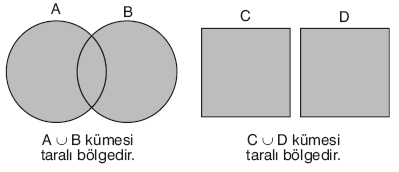
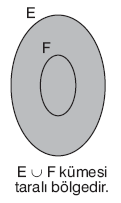 | F Ì E ise, E È F = E dir.E É F ise, E ÈF = E dir. |
2. Birleşim İşleminin Özelikleri
a) A È Æ = A
b) A È A = A
c) A È B = B È A
d) A È (B È C) = (A È B) È C
e) A Ì B ise, A È B = B
f) A È B = Æ ise, (A = Æ ve B = Æ) dir.
3. Kümelerin Kesişimi
A ve B kümesinin ortak elemanlarından oluşan kümeye A ile B nin kesişim kümesi denir ve A Ç B biçiminde gösterilir.
A Ç B = {x : x Î A ve x Î B} dir.
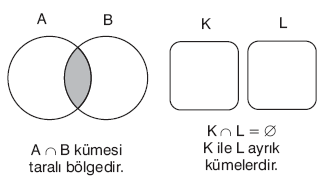
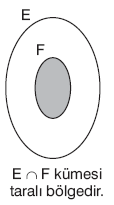 | F Ì E ise, E Ç F = F dir.E É F ise, E ÇF = F dir. |
4. Kesişim İşleminin Özelikleri
a) A Ç Æ = Æ
b) A Ç A = A
c) A Ç B = B Ç A
d) (A Ç B) Ç C = A Ç (B Ç C)
e) A Ç (B È C) = (A Ç B) È (A Ç C)
f) A È (B Ç C) = (A È B) Ç (A È C)
G. EVRENSEL KÜME
Üzerinde işlem yapılan, bütün kümeleri kapsayan kümeye, evrensel küme denir. Evrensel küme genellikle E ile gösterilir.
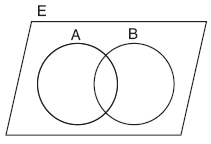 | E Ç A = A dır.E È A = E dir.A ÌE dir.B Ì E dir. |
H. BİR KÜMENİN TÜMLEYENİ
Evrensel kümenin elemanı olup, A kümesinin elemanı olmayan elemanlardan oluşan kümeye A nın tümleyeni denir ve 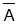 ya da A’ ile gösterilir.
ya da A’ ile gösterilir.
A’ = {x : x Î E ve x Ï A, A Ì E} dir.
Tümleyenin Özelikleri
- Bir kümenin tümleyeninin tümleyeni kendisidir.
Buna göre, (A’)’ = A olur. - Evrensel kümenin tümleyeni boş kümedir. Buna göre, E’ = Æ olur.
- Boş kümenin tümleyeni evrensel kümedir. Buna göre, Æ‘ = E olur.
- Bir kümenin eleman sayısı ile o kümenin tümleyeninin eleman sayısı toplamı evrensel kümenin eleman sayısına eşittir. Buna göre, s(A) + s(A’) = s(E) olur.
- A Ì B ise, B’ Ì A’ dir.
- B’ Ì A’ ise, A Ì B dir.
- E, evrensel küme olmak üzere, A È A’ = E dir.
- A Ç A’ = Æ dir.
- (A È B)’ = A’ Ç B’
- (A Ç B)’ = A’ È B’
- E, evrensel küme olmak üzere, E È A’ = E dir.
- E, evrensel küme olmak üzere, E Ç A’ = A’ dir.
I. KUVVET KÜMESİ
Bir kümenin bütün alt kümelerin kümesine kuvvet kümesi denir. Kuvvet kümesi P(A) ile gösterilir.
s(A) = n ise, s(P(A)) = 2n dir.
J. İKİ KÜMENİN FARKI
A kümesinde olup, B kümesinde olmayan elemanların kümesine A fark B kümesi denir. A fark B kümesi A – B ya da A B biçiminde gösterilir.
A – B = {x : x Î A ve x Ï B} dir.
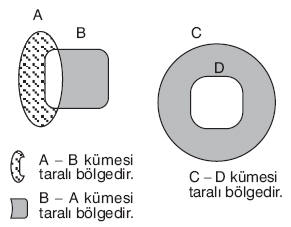
Farkla İlgili Özelikler
A, B, C kümeleri E evrensel kümesinin alt kümeleri olmak üzere,
i) E – A = A’
ii) A – B = A Ç B’
iii) (A – B)’ = A’ È B dir.
iv) (A – B) È (B – A) = A D B (Simetrik Fark)
K. ELEMAN SAYISI
A, B, C herhangi birer küme olmak üzere,
- s(A È B) = s(A) + s(B) – s(A Ç B)
- s(A È B È C) = s(A) + s(B) + s(C) – s(A Ç B) – s(A Ç C)– s(B Ç C) + s(A Ç B Ç C)
- s(A È B) = s(A – B) + s(A Ç B) + s(B – A)
- a + b + c + d tane öğrencinin bulunduğu bir sınıfta voleybol oynayan öğrencilerin sayısı s(V) = b + c, tenis oynayan öğrencilerin sayısı s(T) = a + b, voleybol ve tenis oynayan öğrencilerin sayısı s(T Ç V) = b olsun.
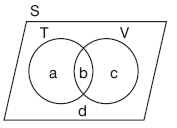 | Şemadaki a, b, c, d bulundukları bölgelerin (kümelerin) eleman sayılarını göstermektedir. |
Tenis veya voleybol oynayanların sayısı:
s(T È V) = a + b + c
Tenis ya da voleybol oynayanların sayısı:
s(T – V) + s(V – T) = a + c
Sadece tenis oynayanların sayısı:
s(T – V) = a
Tenis oynamayanların sayısı:
s(T’) = c + d
Bu iki oyundan en az birini oynayanların sayısı:
s(T È V) = a + b + c
Bu iki oyundan en çok birini oynayanların sayısı:
![]()
Bu iki oyundan hiç birini oynamayanların sayısı:
![]()
Bir apartmanda A gazetesini alan herkes B gazetesini almaktadır. B gazetesini alanlardan C gazetesini alan yoktur.
|