Kartezyen Çarpımı ve Bağıntı konusunu öğrenirken öncelikle bunların ne demek olduğunu ve özelliklerini göreceğiz. Özellikle bağıntı konusunda ki bağıntının özellikleri ve bağıntı çeşitleri konuya hakim olmak açısından göz ardı edilmemesi gerekiyor. Ders notu ve konu anlatımı olarak sizlere sunduğumuz bu bilgileri eksiksiz bir şekilde gözden geçirdiğiniz ve çalıştığınız takdirde soru çözümlerinde kesinlikle zorlanmayacaksınız.
Kartezyen Çarpımı ve Bağıntı konusu Matematik dersinin hemen hemen bütün sınavlarda karşılaşacağınız konularındandır. Konuya iyi bir şekilde çalıştıktan sonra soru çözümüyle pekiştirme yapabilir ve artık bütün soruları çözebilirsiniz.
A. SIRALI n Lİ
n tane nesnenin belli bir öncelik sırasına göre düzenlenip, tek bir nesne gibi düşünülmesiyle elde edilen ifadeye sıralı n li denir.
(a, b) sıralı ikilisinde;
a ya birinci bileşen, b ye ikinci bileşen denir.
| a ¹ b ise, (a, b) ¹ (b, a) dır.(a, b) = (c, d) ise, (a = c ve b = d) dir. |
B. KARTEZYEN ÇARPIM
A ve B herhangi iki küme olmak üzere, birinci bileşeni A kümesinden, ikinci bileşeni B kümesinden alınarak oluşturulan bütün sıralı ikililerin kümesine, A ile B nin kartezyen çarpımı denir.
A kartezyen çarpım B kümesi A ´ B ile gösterilir.
A ´ B = {(x, y) : x Î A ve y Î B} dir.
| A ¹ B ise, A ´ B ¹ B ´ A dır. |
C. KARTEZYEN ÇARPIMIN ÖZELİKLERİ
- 1) s(A) = m ve s(B) = n ises(A ´ B) = s(B ´ A) = m × n dir.
- A ´ (B ´ C) = (A ´ B) ´ C
- A ´ (B È C) = (A ´ B) È (A ´ C)
- (B È C) ´ A = (B ´ A) È (C ´ A)
- A ´ (B Ç C) = (A ´ B) Ç (A ´ C)
- (B Ç C) ´ A = (B ´ A) Ç (C ´ A)
- A ´ Æ = Æ ´ A = Æ

D. BAĞINTI
A ve B herhangi iki küme olmak üzere A ´ B nin her alt kümesine A dan B ye bağıntı denir.
Bağıntı genellikle b ile gösterilir.
b Ì A ´ B ise, b = {(x, y) : (x, y) Î A ´ B} dir.
| s(A) = m ve s(B) = n ise,A dan B ye 2m×n tane bağıntı tanımlanabilir. | |
| A ´ A nın herhangi bir alt kümesine A dan A ya bağıntı ya da A da bağıntı denir. | |
s(A) = m ve s(B) = n olmak üzere,A dan B ye tanımlanabilen r elemanlı (r £ m × n) bağıntı sayısı | |
| b Ì A ´ B olmak üzere,b = {(x, y) : (x, y) Î A ´ B} bağıntısının tersib–1 Ì B ´A dır.Buna göre, b bağıntısının tersib–1 = {(y, x) : (x, y) Î b} dır. |
E. BAĞINTININ ÖZELİKLERİ
b, A da tanımlı bir bağıntı olsun.
1. Yansıma Özeliği
A kümesinin bütün x elemanları için (x, x) Î b ise, b yansıyandır.
“x Î A için, (x, x) Î b ise, b yansıyandır. (“ : Her)
2. Simetri Özeliği
b bağıntısının bütün (x, y) elemanları için (y, x) Î b ise, b simetriktir.
“(x, y) Î b için (y, x) Î b ise, b simetriktir.
| b bağıntısı simetrik ise b = b–1 dir. | |
s(A) = n olmak üzere, A kümesinde tanımlanabilecek simetrik bağıntı sayısı  dir. dir. | |
s(A) = n olmak üzere, A kümesinde tanımlanabilecek yansıyan bağıntı sayısı 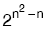 dir. dir. |
3. Ters Simetri Özeliği
b bağıntısı A kümesinde tanımlı olsun.
x ¹ y iken “(x, y) Î b için (y, x) Ï b ise, b ters simetriktir.
| b bağıntısında (x, x) elemanın bulunması ters simetri özeliğini bozmaz. |
4. Geçişme Özeliği
b, A da tanımlı bir bağıntı olsun.
“[(x, y) Î b ve (y, z) Î b] için (x, z) Î b ise,
b bağıntısının geçişme özeliği vardır.
| Boş kümeden farklı bir A kümesinde tanımlanan b = Æ bağıntısında yansıma özeliği yoktur. Simetri, Ters simetri, geçişme özeliği vardır. |
F. BAĞINTI ÇEŞİTLERİ
b bağıntısı A kümesinde tanımlı olsun.
1. Denklik Bağıntısı
b; Yansıma, Simetri, Geçişme özeliğini sağlıyorsa denklik bağıntısıdır.
2. Sıralama Bağıntısı
A kümesinde tanımlı b bağıntısında; Yansıma, Ters simetri, Geçişme özeliği varsa b sıralama bağıntısıdır.
| Bir bağıntı hem denklik, hem de sıralama bağıntısı olabilir |
| b, A kümesinde tanımlı bir denklik bağıntısı olsun. (x, y) Î b ise x ve y elemanları b bağıntısına göre denktir denir ve x º y şeklinde yazılır. | |
b, A kümesinde tanımlı bir denklik bağıntısı olsun. A da x elemanına denk olan bütün elemanların kümesine x in denklik sınıfı denir ve  şeklinde gösterilir. x in denklik sınıfının kümesi, şeklinde gösterilir. x in denklik sınıfının kümesi, |