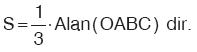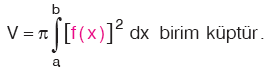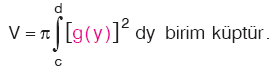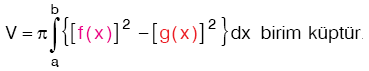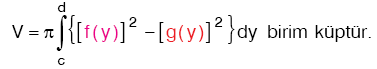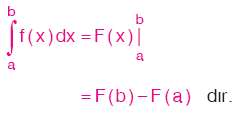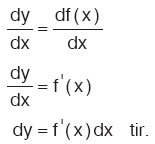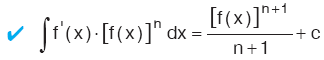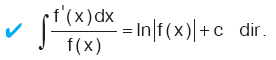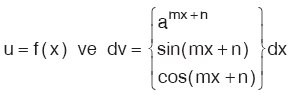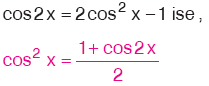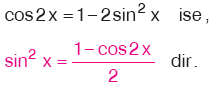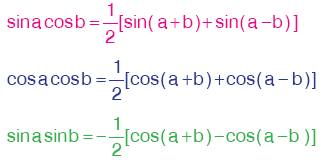Matematik dersinin İntegral konusunda; İntegral ile alan arasındaki ilişki, İntegral ile hacim arasındaki ilişki, belirli İntegral, belirli İntegral’in özellikleri, İntegral – Türev ilişkisi, diferansiyel kavramı, belirsiz İntegral, İntegral alma kuralları, İntegral alma yöntemleri konularını göreceğiz. İntegral aslında türevin tam tersidir. Türev konusunu anlayarak ve öğrendikten sonra İntegral konusuna çalışmaya başladığınız da pek zorlanmayacaksınız.
Aşağıda İntegral konusuna ait ders notu ve konu anlatımı bulunuyor. İntegral konusuna ait bilmeniz gereken bütün bilgiler aşağıda bulunmaktadır. İyi çalışmalar dileriz.
İntegral
A. İNTEGRAL İLE ALAN ARASINDAKİ İLİŞKİ
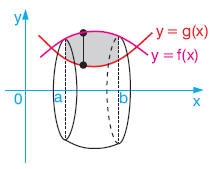
Aşağıdaki şekilde y = f(x) eğrisi y = g(x) eğrisi x = a ve x = b doğrusu arasında kalan taralı bölge verilmiştir.
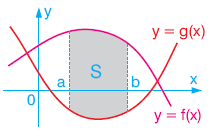
Bölge (ya da eğriler) hangi konumda olursa olsun, yukarıdaki eğrinin denkleminden aşağıdaki eğrinin denkleminin çıkarılmasıyla oluşan belirli integral, bölgenin alanını ifade etmektedir.
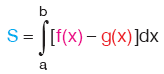
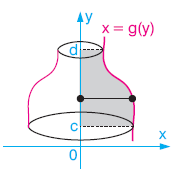
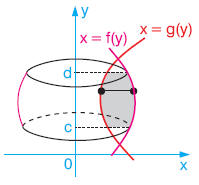
Bu sayfadan sonraki sayfada verilen şekilde x = f(y) eğrisi x = g(y) eğrisi y = a ve y = b doğrusu arasında kalan taralı bölge verilmiştir.
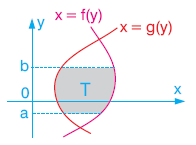
Bölge (ya da eğriler) hangi konumda olursa olsun, sağdaki eğrinin denkleminden soldaki eğrinin denkleminin çıkarılmasıyla oluşan belirli integral, bölgenin alanını ifade etmektedir.
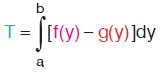
Kural
| 1. Hangi konumda olursa olsun, alan daima pozitif bir reel sayı ile ifade edilir. 2. Belirli integralin değeri bir reel sayıdır. 3. İntegral ile alan ilişkilendirilirken, a. Alan x ekseninin üst kısmındaysa, alanı ifade eden sayı integrali de ifade eder. b. Alan x ekseninin alt kısmındaysa, alanı ifade eden sayının toplama işlemine göre tersi integrali ifade eder. |
Kural
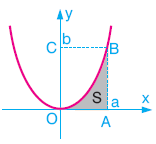
| y = f(x) parabolünün tepe noktasının apsisi r ordinatı k; x = f(y) parabolünün tepe noktasının apsisi n ordinatı m dir. 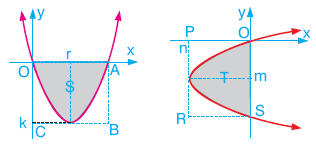 Yukarıda solda verilen parabolde taralı alan, Yukarıda solda verilen parabolde taralı alan,Yukarıda sağda verilen parabolde taralı alan, 
Bu kurallar bütün paraboller için geçerlidir. |
Kural
Şekilde y = f(x) fonksiyonunun grafiği verilmiştir. 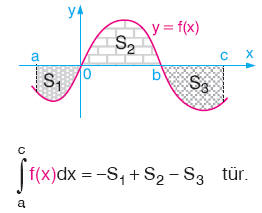 |
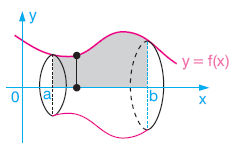
B. İNTEGRAL İLE HACİM ARASINDAKİ İLİŞKİ
Kural
|
Kural
|
Kural
|
Kural
|
A. BELİRLİ İNTEGRAL
![]() olmak üzere, ifadesine f(x) fonksiyonunun
olmak üzere, ifadesine f(x) fonksiyonunun
a dan b ye belirli integrali denir.
Belirli integralin eşiti 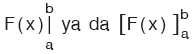 gösterimlerinden biriyle yapılır.
gösterimlerinden biriyle yapılır.
Uyarı
| Daima sadeleşeceği için, integral sabiti olan c belirli integralde yazılmaz. |
B. BELİRLİ İNTEGRALİN ÖZELLİKLERİ
Özellik
 |
Kural
| Mutlak değer, işaret ve tam değer fonksiyonlarının integralleri, fonksiyonun işaret değiştirdiği noktalar göz önüne alınarak sonuçlandırılır. |
Kural
İki ya da daha fazla fonksiyonun toplamının ya da farkının belirli integrali, bu fonksiyonların ayrı ayrı belirli integrallerinin toplamına ya da farkına eşittir. 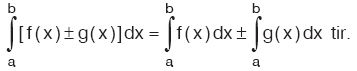 |
Kural
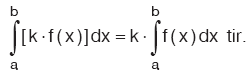 |
C. İNTEGRAL – TÜREV İLİŞKİSİ
Kural
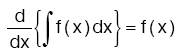 f(x) in integralinin türevi f(x) e eşittir. f(x) in integralinin türevi f(x) e eşittir. |
Kural
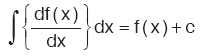 |
Kural
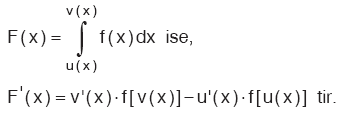 |
A. DİFERANSİYEL KAVRAMI
x in sonsuz küçük değişimi dx şeklinde gösterilir. Buna x değişkeninin diferansiyeli denir.
Fonksiyondaki değişim dy ile gösterilir.
dy = f ‘(x)dx ifadesine y = f(x) fonksiyonunun diferansiyeli denir.
B. BELİRSİZ İNTEGRAL
Türevi f(x) veya diferansiyeli f(x)dx olan F(x) fonksiyonuna f(x) in belirsiz integrali denir ve
şeklinde gösterilir.
∫ sembolüne integral işareti, f(x) fonksiyonundan F(x) + c fonksiyonunun bulunmasını sağlayan işleme integral alma işlemi,
F(x) + c fonksiyonuna da f(x) in ilkel fonksiyonu denir.
Uyarı
| f(x) in integralini bulmak, türevi f(x) e eşit olan fonksiyonu bulmaktır. |
C. İNTEGRAL ALMA KURALLARI
Kural
n ¹ 0 olmak üzere, 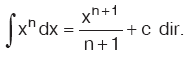 |
Kural
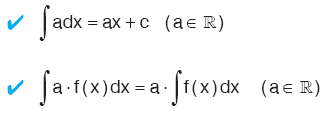 |
Kural
Kural
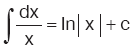 |
Kural
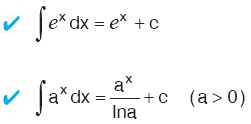 |
Kural
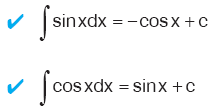 |
Kural
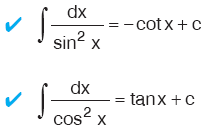 |
Kural
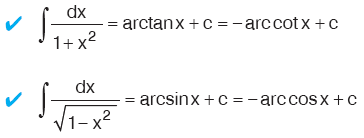 |
D. İNTEGRAL ALMA YÖNTEMLERİ
1. Değişken Değiştirme Yöntemi
İntegrali alınan fonksiyon f(u)du gibi daha basit bir ifadeye dönüştürülerek integral alınır.
Kural
| n ¹ –1 olmak üzere, |
Kural
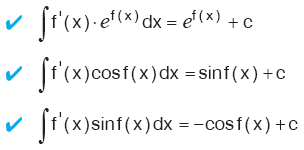 |
Kural
Kural
Kural
Kural
2. Kısmî İntegrasyon Yöntemi
u = f(x)
v = g(x)
olsun. u × v nin diferansiyeli,
d(u × v) = du × v + dv × u
olur. Buradan,
u × dv = d(u × v) – v × du
olur. Her iki tarafın integrali alınırsa,
Uyarı
| Kısmî integralde u nun ve dv nin doğru seçilmesi çok önemlidir. Seçim doğru yapılmazsa, çözüme yaklaşmak yerine, çözümden uzaklaşılır. Türev ve integral alma bilgileri ışığında, seçim sezgisel olarak yapılabilir. Ancak, kolaylık sağlayacağı için aşağıdaki kuralı göz önüne alabilirsiniz. |
Kural
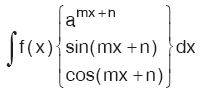 |
Sonuç
n bir doğal sayı olmak üzere,  f(x) bir polinom fonksiyon olmak üzere, f(x) bir polinom fonksiyon olmak üzere, 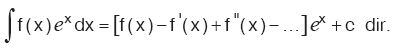 |
3. Basit Kesirlere Ayırma Yöntemi
P(x) ve Q(x) ortak çarpanı olmayan iki polinom olsun.
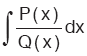 integrali, vereceğimiz iki yöntemden biriyle sonuçlandırılır.
integrali, vereceğimiz iki yöntemden biriyle sonuçlandırılır.
a. P(x) in derecesi Q(x) in derecesinden büyük ya da eşit ise;
P(x) in derecesi Q(x) in derecesinden büyük ya da eşit ise P(x), Q(x) e bölünür.
b. P(x) in derecesi Q(x) in derecesinden küçük ise;
P(x) in derecesi Q(x) in derecesinden küçükse ifade basit kesirlere ayrılır.
4. Trigonometrik Özdeşliklerden Yararlanarak İntegral Alma Yöntemi
Kural
| sin x ve cos x in çift kuvvetlerinin çarpımı biçimindeki integrallerde şu iki özdeşlik kullanılır: |
Kural
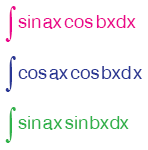 biçimindeki integralleri aşağıdaki özdeşlikler yardımıyla sonuçlandırırız. |