Matematik dersinin İkinci Dereceden Denklemler konusunda; İkinci Dereceden Denklemlerin tanımı, İkinci Dereceden Denklemlerin kökleri, çözüm kümesi, kat sayıları, çarpanlara ayırma yöntemi, diskiriminant yöntemi, İkinci Dereceden Denklemin kökleri ile katsayıları arasındaki bağıntılar, kökleri verilen İkinci Dereceden Denklemin yazılması, üçüncü dereceden denklemler, kökleri verilen üçüncü dereceden denklemin yazılması, Üçüncü Dereceden Denklemin kökleri ile katsayıları arasındaki bağıntılar konularını göreceğiz.
Aşağıda İkinci Dereceden Denklemler konusuna ait ders notu ve konu anlatımı bulunmaktadır. İkinci Dereceden Denklemler konusuna ait bilinmesi gereken bütün bilgileri aşağıda sizler için derledik. İyi çalışmalar dileriz.
İkinci Dereceden Denklemler
A. TANIM
a, b, c gerçel sayı ve a ¹ 0 olmak üzere,
ax2 + bx + c = 0
biçimindeki her açık önermeye ikinci dereceden bir bilinmeyenli denklem denir.
Bu açık önermeyi doğrulayan x sayılarına denklemin kökleri; tüm köklerin oluşturduğu kümeye denklemin çözüm kümesi; çözüm kümesini bulmak için yapılan işlemlere denklem çözme; a, b, c sayılarına da denklemin kat sayıları denir.
B. İKİNCİ DERECE DENKLEMİN ÇÖZÜM KÜMESİNİN BULUNUŞU
1. Çarpanlara Ayırma Yöntemi
ax2 + bx + c = 0 denklemi f(x) . g(x) = 0
biçiminde yazılabiliyorsa
f(x) = 0 veya g(x) = 0 olup çözüm kümesi;
Ç = {x | x, f(x) = 0 veya Q(x) = 0 denklemini sağlar} olur.
2. Diskiriminant (D) Yöntemi
ax2 + bx + c = 0 denklemi a ¹ 0 ve
D = b2 – 4ac ise, çözüm kümesi
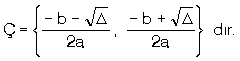 |
ax2 + bx + c = 0
denkleminde, D = b2 – 4ac olsun.
a) D > 0 ise, denklemin farklı iki gerçel kökü vardır.
| Bu kökleri, | 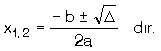 |
b) D < 0 ise, denklemin gerçel kökü yoktur.
c) D = 0 ise, denklemin eşit iki gerçel kökü vardır.
| Bu kökler, |
Denklemin bu köklerine; eşit iki kök, çakışık kök ya da çift katlı kök denir.
Ü ax2 + bx + c = 0
denkleminin kökleri simetrik ise,
1) b = 0 ve a ¹ 0 dır.
2) Simetrik kökleri gerçel ise,
b = 0, a ¹ 0 ve a . c £ 0 dır.
C. İKİNCİ DERECE DENKLEMİN KÖKLERİ İLE KATSAYILARI ARASINDAKİ BAĞINTILAR
ax2 + bx + c = 0 denkleminin kökleri
x1 ve x2 ise,
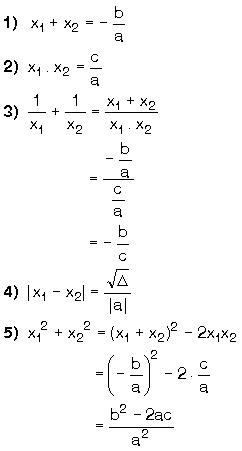 |
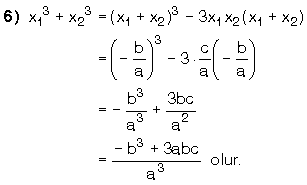 |
D. KÖKLERİ VERİLEN İKİNCİ DERECEDEN DENKLEMİN YAZILMASI
Kökleri x1 ve x2 olan ikinci dereceden denklem;
(x – x1) (x – x2) = 0 dır. Bu ifade düzenlenirse,
x2 – (x1 + x2)x + x1x2 = 0 olur.
Ü ax2 + bx + c = 0 … (1) denkleminin kökleri x1 ve x2 olsun. Kökleri mx1 + n ve
mx2 + n olan ikinci dereceden denklem, (1) denkleminde x yerine
yazılarak bulunur.
Ü ax2 + bx + c = 0 ve dx2 + ex + f = 0 denklemlerinin çözüm kümeleri aynı ise,
![]()
Ü ax2 + bx + c = 0 ve dx2 + ex + f = 0
denklemlerinin sadece birer kökleri eşit ise,
ax2 + bx + c = dx2 + ex + f
(a – d)x2 + (b – e)x + c – f = 0 dır.
Bu denklemin kökü verilen iki denklemi de sağlar.
ÜÇÜNCÜ DERECEDEN DENKLEMLER
A. TANIM
a ¹ 0 olmak üzere, ax3 + bx2 + cx + d = 0 biçimindeki denklemlere üçüncü dereceden bir bilinmeyenli denklemler denir.
B. ÜÇÜNCÜ DERECEDEN DENKLEMİN KÖKLERİ İLE KATSAYILARI ARASINDAKİ BAĞINTILAR
a ¹ 0 ve ax3 + bx2 + cx + d = 0 denkleminin kökleri x1, x2 ve x3 olsun. Buna göre,
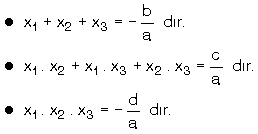 |
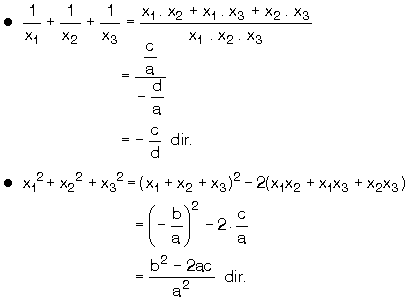 |
C. KÖKLERİ VERİLEN ÜÇÜNCÜ DERECE DENKLEMİN YAZILMASI
Kökleri x1, x2 ve x3 olan üçüncü derece denklem
(x – x1) (x – x2) (x – x3) = 0 dır.
Bu denklem düzenlenirse,
x3 – (x1 + x2 + x3)x2 + (x1x2 + x1x3 + x2x3)x – x1x2x3 = 0
olur.
Ü ax3 + bx2 + cx + d = 0 denkleminin kökleri
x1, x2, x3 olsun.
1) Bu kökler aritmetik dizi oluşturuyorsa,
x1 + x3 = 2x2 dir.
2) Bu kökler geometrik dizi oluşturuyorsa,
3) Bu kökler hem aritmetik hem de geometrik dizi oluşturuyorsa,
x1 = x2 = x3 tür.
n, 1 den büyük pozitif tam sayı olmak üzere,
anxn + an – 1xn – 1 + … + a1x + a0 = 0
denkleminin;
Kökleri toplamı : 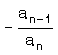
Kökleri çarpımı : 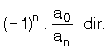

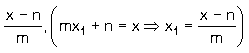 yazılarak bulunur.
yazılarak bulunur.