Hacim Hesaplaması Nasıl Yapılır? Küp, Silindir, Küre, Piramit Gibi Şekillerin Hacim Formülleri

Hacimin Tanımı ve Hesaplanması;

Her hangi bir cisim uzayda bir yer kaplıyorsa kapladığı bu alana hacim denilmektedir. Normal şartlarda bir cismin hacmini hesaplamak için cismin enini, boyunu ve yüksekliğini çarparız. Yani (en) X (boy) X (yükseklik). Ama öyle şekiller karşımıza çıkıyor ki bu şeklin enini, boyunu veya yüksekliği düzgün olmuyor. Örneğin; piramit, küre veya silindir.

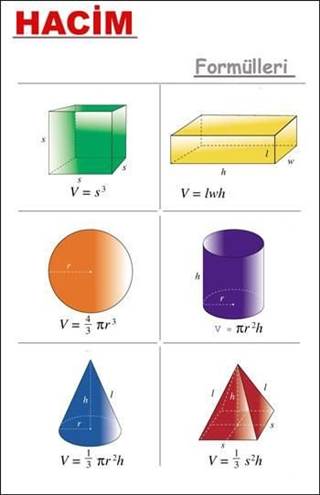
Bazı Şekillerin Hacim Formülleri;

Küpün hacim formülü; Küpün bir kenarına “a” dersek; hacmi “a üzeri 3” olur. (bir kenara 5 dersek 5 üzeri 3 = 5 X 5 X 5 = 125 gibi.)

Silindirin hacim formülü; Pi sayısı X silindirin tabanının yarıçapının karesi X silindirin yüksekliği

Prizmanın hacim formülü; Prizma tabanının alanı X prizmanın yüksekliği

Dikdörtgenler prizmasının hacim formülü; prizmanın eni X boyu X yüksekliği

Kürenin hacim formülü; (4 / 3) X pi sayısı X kürenin yarıçapı üzeri 3 (yarıçapa 5 dersek; 5 üzeri 3 = 5 X 5 X 5 = 125 gibi.)

Elipsoitin hacim formülü; (4 / 3) X pi sayısı X a ekseni X b ekseni X c ekseni

Piramitin hacim formülü; (1 / 3) X taban alanı X yükseklik

Koninin hacim formülü; (1 / 3) X pi sayısı X yükseklik X koninin yarıçapı üzeri 2 (yarıçapa 5 dersek; 5 üzeri 2 = 5 X 5 = 25 gibi.)

Düzgün dörtyüzlünün hacim formülü; (kök 2 / 12) X a üzeri 3 (bir kenara 5 dersek 5 üzeri 3 = 5 X 5 X 5 = 125 gibi.)