Geometrik Uzay Ders Notu ve Konu Anlatımı

Geometri dersinin Geometrik Uzay konusunda; noktanın tanımı, doğrunun tanımı, düzlemin tanımı, düzlemle doğrunun durumları, düzlemde iki doğrunun birbirine göre durumları, düzlemde üç doğrunun birbirine göre durumları, düzlemde nokta ile doğrunun durumları, doğruların düzlemde ayırdığı bölge sayısı, uzayın tanımı, uzay belirtme aksiyomları gibi konuları göreceğiz.

Sponsorlu Bağlantılar

Geometrik Uzay konusuna ait ders notu ve konu anlatımlarını aşağıda bulabilirsiniz. Geometrik Uzay konusu ile ilgili bilinmesi gereken bütün bilgileri bu sayfada bulabilirsiniz. İyi çalışmalar dileriz.

Geometrik Uzay

BAZI KAVRAM ve TANIMLAR

Geometride nokta, doğru, düzlem ve uzay gibi bazı kavramlar tanımsız olarak kabul edilir. Kalemin veya sivri bir şeyin ucunun bıraktığı ize nokta diyebiliriz. Cetvelin kenarı ile bir doğru çizebiliriz. Sınıfın duvarı, pencere camı birer düzlemdir. Odanın içerisi, herhangi bir cisminkapladığı yer birer uzay belirtirler.

Nokta : « . » Biçiminde ifade edilir ve genellikle büyük harfle gösterilir. Nokta boyutsuzdur.

« . » nokta, « . A” A noktası

Doğru : iki ucuna ok işareti koyulmuş düz bir çizgi ile gösterilir. Doğru küçük harfle veya üzerindeki iki nokta ile gösterilir.

Sponsorlu Bağlantılar

d »d doğrusu

veya AB doğrusu diye okunur. Buradaki A ve B noktaları doğrunun birer elemanıdır.

A Îd ve B Î d biçiminde yazılır.

Farklı iki noktadan bir tek doğru geçer.
Farklı iki nokta bir tek doğru belirtir.

Doğru bir boyutludur. Yani sadece uzunluk söz konusudur.

Düzlem: Uzunluğuna ve genişliğine doğru sonsuza uzayıp giden düz bir yüzeydir. Düzlem iki boyutludur. Sayfa üzerinde paralelkenar gibi gösterilebilir. Paralelkenarın köşesine harfle ismi yazılabilir.

şekildeki düzlem E düzlemi diye isimlendirilir.

Burada A, B ve C noktaları E düzlemi üzerindedir. Dolayısıyla B ve C noktalarından geçen d doğrusu da E düzlemi üzerindedir.

A Î E

B Î E

C Î E

d Î E

Aynı doğru üzerinde olmayan farklı üç nokta bir düzlem belirtir.
Bir doğru ile, bu doğru üzerinde olmayan bir nokta, bir düzlem belirtir.
Bir doğrunun farklı iki noktası bir düzlem üzerinde ise bu doğru (doğrunun bütün noktaları) bu düzlem üzerindedir.

1. Düzlemle Doğrunun Durumları

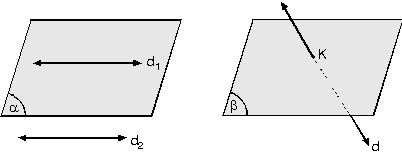Bir doğru düzlemin ya üzerinde, ya dışındadır veya düzlemi bir noktada keser.

d₁Ça = d₁

d₂Ç a = Ø

d Çb = {K}

K noktası kesişen bir doğru ile bir düzlemin arakesitidir.

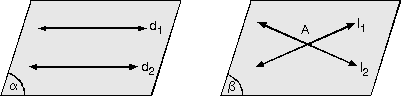
2. Düzlemde İki Doğrunun Birbirine Göre Durumları

Paralel farklı iki doğru bir tek düzlem belirtir.
Her paralel farklı iki doğrudan bir tek düzlem geçer.
Kesişen farklı iki doğru bir tek düzlem belirtir. Her kesişen farklı iki doğrudan bir tek düzlem geçer.
Bir düzlemde farklı iki doğru ya paraleldir, ya da bir noktada kesişirler.

d₁ Ç d₂ = Ø

l₁ Ç l₂ = {A}

Üst üste çizilen çakışık doğrular bir tek doğru kabul edilir.

3. Düzlemde Üç Doğrunun Birbirlerine Göre Durumları

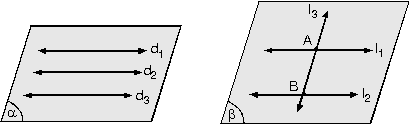Üç doğru paralel olabilir.

d₁ // d₂ // d₃ d₁Ç d₂Çd₃ = Ø

Düzlemde paralel olan iki doğrudan birine paralel olan doğru diğerine de paraleldir.

d₁ // d₂ ve d₂ // d₃ ise d₁ // d₃ olur.

Yalnız ikisi paralel ise, üçüncü doğru paralel doğruları birer noktada keser.

l₁ // l₂

l₁Ç l₃ = {A}

l₂Ç l₃ = {B}

Düzlemde paralel iki doğrudan birini kesen bir doğru, diğerini de keser.
Düzlemde paralel iki doğrudan birini dik kesen bir doğru diğerini de dik keser.

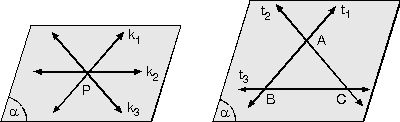Üç doğru bir noktada kesişebilir.

k₁Ç k₂Çk₃ = {P}

Üç doğru ikişer ikişer kesişebilir.

t₁Ç t₂ = {A}

t1 Ç t3 = {B}

t2 Ç t3 = {C}

t1 Ç t2 Çt3 = Ø

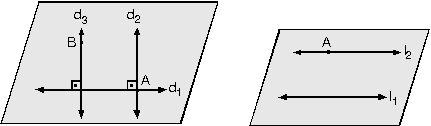
4.Düzlemde Nokta İle Doğrunun Durumları

Doğrunun üzerindeki bir noktadan geçen ve bu doğruya dik olan bir tek doğru çizilebilir.

d₂ doğrusu A’dan geçer ve d₁ e diktir

Doğrunun dışındaki bir noktadan geçen ve bu doğruya dik olan bir tek doğru çizilebilir.

d₃ doğrusu B’den geçer ve d1 e diktir.

Doğrunun dışındaki bir noktadan geçen ve bu doğruya paralel olan bir tek doğru çizilebilir.

l₂ doğrusu A’dan geçer ve l1 ile paraleldir.

5. Doğruların Düzlemde Ayırdığı Bölge Sayısı

Genel olarak, n adet doğru bir düzlemi en az (n + 1) bölgeye (paralellik hali), en

fazla

bölgeye ayırır.

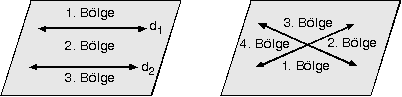İki doğru, bir düzlemi en az 3 bölgeye, en fazla 4 bölgeye ayırır.

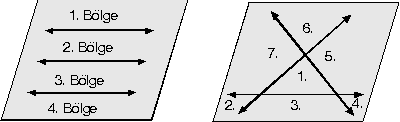Üç doğru, bir düzlemi en az 4 bölgeye, en fazla 7 bölgeye ayırır.

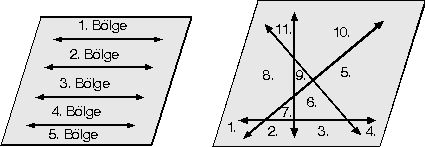Dört doğru, bir düzlemi en az 5 bölgeye, en fazla 11 bölgeye ayırır.

UZAY KAVRAMI VE UZAYDA DOĞRULAR

Cisimlerin kapladığı yer ve içinde bulundukları mekan uzaydır. Doğruda sadece uzunluk, düzlemde uzunluk ve genişlik söz konusu idi. Uzayda ise uzunluk ve genişliğin yanında bir de yükseklik kavramı vardır. (Derinlikte denilebilir.) Dolayısıyla uzay üç boyutludur. Uzayda x, y, z eksenleri olduğu için kartezyen koordinat olarak R x R x R veya R³ ile sembolize edilir.

Aşağıda üç boyutlu cisimlerin bazıları belirtilmiştir.

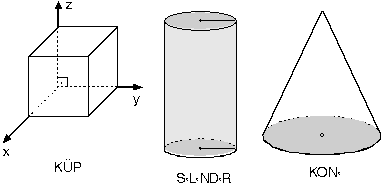1. Uzay Belirtme Aksiyomları

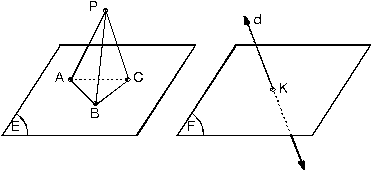Dördü aynı düzlemde bulunmayan farklı dört nokta uzay belirtir.

E düzlemindeki A, B, C noktaları ile düzlem dışındaki P noktası, uzay belirtir.

Sponsorlu Bağlantılar

Bir düzlem ile bu düzlemin dışındaki bir nokta, uzay belirtir.

E düzlemi ile bu düzlemin dışındaki P noktası uzay belirtir.

Bir düzlem ve düzlem üzerinde olmayan bir doğru uzay belirtir.

d doğrusu F düzleminde olmadığından, F düzlemi ile d doğrusu uzay belirtir.

Uzayda farklı iki düzlem ya paraleldir ya da kesişirler.
Paralel olmayan farklı iki düzlem daima kesişir.
Farklı iki düzlem daima uzay belirtir.
Kesişen iki düzlemin ortak noktalarının oluşturduğu doğruya arakesit doğrusu denir.

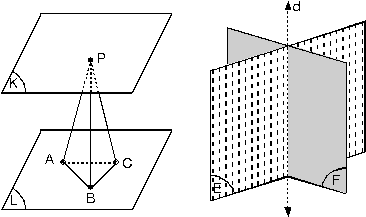Farklı K ve L düzlemleri uzay belirtir. E ve F düzlemlerinin kesişim kümesi d doğrusudur. E Ç F = d dir.

Sponsorlu Bağlantılar

Geometrik Uzay

Bir yanıt yazın Yanıtı iptal et