Çarpanlarına Ayırma
Çarpanlara Ayırma konusunda ortak paranteze alma, özdeşlikler (iki kare farklı – toplamı, iki küp farkı, 2.dereceden farkı, n.dereceden farkı, tam kare ifadeler, pascal üçgeni gibi ifadeler bulunmaktadır.
Çarpanlara ayırma konusuna ait matematik sorularını sorunsuz bir şekilde çözebilmeniz için çarpanlara ayırmanın özelliklerini kesinlikle bilmeniz gerekmektedir. Özellikleri öğrendikten sonra soruları daha kolay anlayacak ve soruları hangi yolla çözmeniz gerektiğini bileceksiniz.
A. ORTAK ÇARPAN PARANTEZİNE ALMA

| En az dört terimi olan ifadeler ortak çarpan parantezine alınacak şekilde bir araya getirilir, ardından ortak çarpan parantezine alınır. |
B. ÖZDEŞLİKLER
1. İki Kare Farkı – Toplamı
1) a2 – b2 = (a – b)(a + b)
2) a2 + b2 = (a + b)2 – 2ab
3) a2 + b2 = (a – b)2 + 2ab
2. İki Küp Farkı – Toplamı
1) a3 – b3 = (a – b)(a2 + ab + b2 )
2) a3 + b3 = (a + b)(a2 – ab + b2 )
3) a3 – b3 = (a – b)3 + 3ab(a – b)
4) a3 + b3 = (a + b)3 – 3ab(a + b)
3. n. Dereceden Farkı – Toplamı
1) n bir sayma sayısı olmak üzere,
xn – yn = (x – y)(xn – 1 + xn – 2y + xn – 3 y2 + … + xyn – 2 + yn – 1) dir.
2) n bir tek sayma sayısı olmak üzere,
xn + yn = (x + y)(xn – 1 – xn – 2y + xn – 3 y2 – … – xyn – 2 + yn – 1) dir.
4. Tam Kare İfadeler
1) (a + b)2 = a2 + 2ab + b2
2) (a – b)2 = a2 – 2ab + b2
3) (a + b + c)2 = a2 + b2 + c2 + 2(ab + ac + bc)
4) (a + b – c)2 = a2 + b2 + c2 + 2(ab – ac – bc)
| n bir tam sayı ve a ¹ b olmak üzere,• (a – b)2n = (b – a)2n• (a – b)2n – 1 = –(b – a)2n – 1 dir. |
| • (a + b)2 = (a – b)2 + 4ab |
5. (a ± b)n nin Açılımı
Pascal Üçgeni

(a + b)n açılımı yapılırken, önce a nın n. kuvvetten başlayarak azalan, b nin 0 dan başlayarak artan kuvvetlerinin çarpımları yazılıp toplanır.
Sonra n’nin Paskal üçgenindeki karşılığı bulunarak kat sayılar belirlenir.
(a – b)n yukarıdaki biçimde yapılır ancak b nin; çift kuvvetlerinde terimin önüne (+), tek kuvvetlerinde terimin önüne (–) işareti konulur.
| • (a + b)3 = a3 + 3a2b + 3ab2 + b3• (a – b)3 = a3 – 3a2b + 3ab2 – b3• (a + b)4 = a4 + 4a3b + 6a2b2 + 4ab3+b4• (a – b)4 = a4 – 4a3b + 6a2b2 – 4ab3 + b4 |
| • a4 + a2 + 1 = (a2 + a + 1)(a2 – a + 1)• a4 + 4 = (a2 + 2a + 2)(a2– 2a + 2)• a4 + 4b4 = (a2 + 2ab + 2b2)(a2 – 2ab + 2b2) |
| a3 + b3 + c3 – 3abc = (a + b + c)(a2 + b2 + c2 – ab – ac – bc) |
C. ax2 + bx + c BİÇİMİNDEKİ ÜÇ TERİMLİNİN ÇARPANLARA AYRILMASI
ax2 + bx + c ifadesini çarpanlarına ayırırken birkaç yöntem kullanılır. Biz burada ikisini vereceğiz. En iyi öğrendiğiniz yöntemi daima kullanarak pratiklik sağlayınız.
1. YÖNTEM
1. a = 1 için,
b = m + n ve c = m × n olmak üzere,

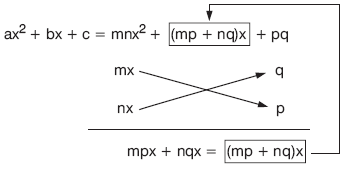
2. a ¹ 1 İken
m × n = a, mp + qn = b ve c = q × p ise

ax2 + bx + c = (mx + q) × (nx + p) dir.
2. YÖNTEM
Çarpımı a × c yi, toplamı b yi veren iki sayı bulunur. Bulunan sayılar p ve r olsun. Bu durumda,