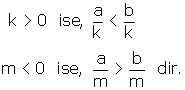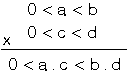Matematik dersinin Basit Eşitsizlikler konusunda; büyüktür ve küçüktür gibi ifadeleri öğreneceğiz, kapalı aralık, açık aralık, yarı açık aralık gibi tanımların ne demek olduğunu göreceğiz, eşitsizliklerde yapacağımız işlemler için eşitsizliklerin özelliklerini göreceğiz. Aşağıda Basit Eşitsizlikler konusuna ait ders notu ve konu anlatımı bulunmaktadır. Basit Eşitsizlikler konusu ile ilgili bütün bilgileri bu sayfada bulabilirsiniz. Ders notu ve konu anlatımına çalıştıktan sonra hızlı bir şekilde soru çözümlerine başlayabilirsiniz. İyi çalışmalar dileriz.
Basit Eşitsizlikler
Reel sayıları “<” ya da “>” sembolleriyle yapılan karşılaştırmaya reel sayıların eşitsizlikleri denir.
> : Büyüktür.
< : Küçüktür.
³ : Büyük veya eşittir.
£ : Küçük veya eşittir.
A. REEL (GERÇEK) SAYI ARALIKLARI
1. Kapalı Aralık
a < b olsun.
a ve b sayıları ile bu sayıların arasındaki tüm reel (gerçek) sayıları kapsayan aralık
a £ x £ b, x Î R biçiminde gösterilir ve “a, b kapalı aralığı” diye okunur. Ve sayı doğrusu üzerinde yukarıdaki gibi gösterilir.
2. Açık Aralık ve Yarı Açık Aralık
a < x < b, x Î R ifadesine açık aralık denir. Ve sayı doğrusu üzerinde yukarıdaki gibi gösterilir.
- Açık aralığının uç noktalarından herhangi birinin dahil edilmesiyle elde edilen aralığa yarı açık aralık denir.
a £ x < b ifadesi sayı doğrusu üzerinde yukarıdaki gibi gösterilir.
B. EŞİTSİZLİĞİN ÖZELİKLERİ
- Bir eşitsizliğin her iki yanına aynı sayı eklenir ya da çıkarılırsa eşitsizlik aynı kalır.
a + c <b+c ve
a – d < b-d dir
- Bir eşitsizliğin her iki yanı pozitif bir sayı ile çarpılırsa ya da bölünürse eşitsizlik aynı kalır. Negatif sayı ile çarpılırsa ya da bölünürse eşitsizlik yön değiştirir.
c > 0 ise, a . c <b.c
d < 0 ise, a . d >b.d
- a < b < 0 ise, 0 > 1/a > 1/b dir.
- 0 < a < b ve n Î N+ ise, an < bn dir.
- a < b < 0 ve n Î N+ ise, a2n > b2n
(2n : Çift doğal sayıdır.)
(2n+1 : Tek doğal sayıdır.)
- a < b ve b < c Ş a < c dir.
- a . b < 0 ise,
a ile b zıt işaretlidir.
- a . b > 0 ise,
a ile b aynı işaretlidir.